Аннотация
Выдающийся русский философ Алексей Лосев, исследователь эстетики античности и эпохи Возрождения, в следующих словах сформулировал «золотую» парадигму древних греков: «С точки зрения Платона, да и вообще с точки зрения всей античной космологии мир представляет собой некое пропорциональное целое, подчиняющееся закону гармонического деления - золотого сечения». Новейшие открытия современной науки, основанные на Платоновых телах, золотом сечении, числах Фибоначчи: фуллерены, Нобелевская Премия – 1996; квазикристаллы, Нобелевская Премия – 2011; экспериментальное доказательство существования гармонии «золотого сечения» в квантовом мире; обнаружение фибоначчиевой закономерности в таблице Менделеева; «гипотеза Прокла» и новый взгляд на «Начала» Евклида и историю развития математики, начиная с Евклида; гиперболические фунции Фибоначчи и новая геометрическая теория филлотаксиса; треугольник Паскаля и обобщенные числа Фибоначчи; обобщенные золотые пропорции и закон структурной гармонии систем; лямбда-числа Фибоначчи как новый класс целочисленных последовательностей, обладающих уникальными математическими свойствами; «металлические пропорции» и общая теория гармонических гиперболических функций; решение четвертой проблемы Гильберта и поиск гармонических гиперболических миров Природы; "золотые" матрицы, преобразования Фибоначчи-Лоренца и «золотая» интерпретация специальной теории относительности; «золотые» геноматрицы; алгоритмическая теории измерений, коды и компьютеры Фибоначчи; системы счисления с иррациональными основаниями, троичная зеркально-симметричная арифметика и "золотая" теория чисел как новое направление в теории чисел; обобщенные матрицы Фибоначчи и новая теория кодирования; наконец, «математика гармонии» как новое междисциплинарное направление, восходящее к «Началам» Евклида, - все это «лики божественной пропорции» в современной науке, которые создают общую картину ее движения к "Золотой" Научной Революции, что в совокупности отражает одну из важнейших тенденций в развитии современной науки – возврат к Пифагору, Платону и Евклиду.
Часть II
«Математика владеет не только истиной, но и высокой красотой – красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства».
Бертран Рассел
Предисловие
Каждому из нас не раз приходилось задумываться над тем, почему Природа способна создавать такие удивительные эстетические структуры, которые восхищают и радуют глаз. Почему художники, поэты, композиторы, архитекторы создают восхитительные произведения искусства из столетия в столетие? В чем же секрет и какие законы лежат в основе этих гармоничных созданий? Что такое «гармония»? И имеет ли она математическое выражение? Для моделирования «мира гармонии» в античном мире, прежде всего в Древней Греции, была создана математика гармонии, элементы которой возрождены в современной науке во многих книгах [1 - 25], включая книгу Alexey Stakhov “The Mathematics of Harmony. From Euclid to Contemporary Mathematics and Computer Science”, опубликованной в 2009 г. одним из наиболее престижных научных издательств мира “World Scientific” [25].
Цель настоящей публикации, предназначенной для широкой аудитории, состоит в том, чтобы популярно объяснить понятие «гармонии», которое было введено в науку на заре развития человеческой цивилизации, рассказать об истории этого направления в античный период, эпоху средневековья, эпоху Возрождения, в 19 и 20 веках, а также ввести в круг идей и приложений современной «математики гармонии», автивно развивающейся в 21 в. [25]. Конечно, «математика гармонии» - это раздел математики; поэтому полностю избежать математических формул в статье, посвященной этой математической дисциплине, авторам не удалось. Однако, «математика гармонии» - это достаточно простая (можно сказать, «элементарная») математика, в которой используются математические формулы, доступные школьникам старших классов. И авторы надеются на снисхождение наших читателей.
Статья состоит из 4-х частей:
Часть II. Числа Фибоначчи и 10-я проблема Гильберта
Часть III. Платоновы тела, «гипотеза Прокла», новый взгляд на «Начала» Евклида, фуллерены и квазикристаллы
Часть IV. Роль «математики гармонии» в развитии современной науки
Часть II. Числа Фибоначчи и 10-я проблема Гильберта
6. Числа Фибоначчи
Кто такой Фибоначчи?
С понятием «средневековье» в нашем сознании ассоциируется разгул инквизиции, костры, на которых сжигали ведьм и еретиков, крестовые походы за «телом господним». Наука в те времена явно не находилась «в центре внимания общества». В этих условиях появление книги по математике “Liber abaci” («Книга об абаке»), написанной в 1202 году итальянским математиком Леонардо из Пизы (по прозвищу Фибоначчи), явилось важным событием в «научной жизни общества».
О жизни Фибоначчи известно немного. Неизвестна даже точная дата его рождения. Предполагается, что Фибоначчи родился в восьмой декаде 12-го столетия (предположительно в 1170 г.). Его отец был купцом и государственным чиновником, представителем нового класса бизнесменов, порожденных «Коммерческой Революцией». В то время Пиза была одним из крупнейших коммерческих центров, активно сотрудничавших с исламским Востоком, и отец Фибоначчи активно торговал в одной из факторий, основанных итальянцами на северном побережье Африки. Благодаря этому обстоятельству ему удалось «пристроить» своего сына, будущего математика Фибоначчи, в одно из арабских учебных заведений, где он смог получить неплохое для того времени математическое образование.
Один из известных историков математики Морис Кантор назвал Фибоначчи «блестящим метеором, промелькнувшим на темном фоне западно-европейского средневековья».
Хотя Фибоначчи был одним из наиболее ярких математических умов в истории западноевропейской математики и внес огромный вклад в ее развитие, однако его вклад в математику незаслуженно принижен. Наиболее убедительно значение математического творчества Фибоначчи для математики отмечено русским математиком проф. А.В. Васильевым в его книге «Целое число» (1919 г.):
«Сочинения ученого пизанского купца были настолько выше уровня математических знаний даже ученых того времени, что их влияние на математическую литературу становится заметным только через два столетия после его смерти в конце 15-го века, когда многие из его теорем и задач вводятся другом Леонардо да Винчи, профессором многих итальянских университетов Лукою Пачоли в его сочинениях и в начале 16-го века, когда группа талантливых итальянских математиков: Сципион дель Ферро, Иероним Кардано, Тарталия, Феррари решением кубического и биквадратного уравнения положили начало высшей алгебре».
Из этого высказывания вытекает, что Фибоначчи почти на два столетия опередил западноевропейских математиков своего времени. Подобно Пифагору, который получил свое «научное образование» у египетских и вавилонских жрецов и затем способствовал передаче полученных знаний в греческую науку, Фибоначчи получил свое математическое образование в арабских учебных заведениях и многие из полученных там знаний, в частности, арабо-индусскую десятичную систему счисления, он попытался «внедрить» в западноевропейскую науку. И подобно Пифагору, историческая роль Фибоначчи для западного мира состояла в том, что он своими математическими книгами способствовал передаче математических знаний арабов в западноевропейскую науку и тем самым заложил основы для дальнейшего развития западноевропейской математики.
Рекуррентное соотношение Фибоначчи
По иронии судьбы, Фибоначчи, который внес выдающийся вклад в развитие математики (об этом, кстати, пишет Колмогоров в своей книге [27]), стал известным в современной математике только лишь как автор интересной числовой последовательности, называемой числами Фибоначчи [1 - 4]. Эта числовая последовательность была получена Фибоначчи при решении “задачи о размножении кроликов», прославившей Фибоначчи. Формулировка и решение этой задачи считается основным вкладом Фибоначчи в развитие комбинаторики. Именно с помощью этой задачи Фибоначчи предвосхитил метод рекуррентных соотношений, который позже стал одним из мощных методов решения комбинаторных задач. Рекуррентная формула, полученная Фибоначчи при решении этой задачи, считается первой в истории математики рекуррентной формулой
Fn= Fn-1+ Fn-2. (12)
Если принять начальные условия
F1= F2=1, (13)
и произвести вычисления согласно (12), то при этом возникает следующая числовая последовательность:
1,1,2,3,5,8,13,21,34,55,89,144,233, ... . (14)
называемая в математике числами Фибоначчи [1 - 4].
Некоторые математические тождества для чисел Фибоначчи
Теория чисел Фибоначчи описана в прекрасных книгах [2 - 4]. Мы остановимся только на некоторых свойствах чисел Фибоначчи, чтобы показать важность чисел Фибоначчи для математики и науки и подчеркнуть эстетические аспекты этой замечательной числовой последовательности.
Расширенные числа Фибоначчи. Последовательность Фибоначчи Fn может быть расширена в сторону отрицательных значений индекса n (F-n). При этом возникает бесконечная целочисленная последовательность в пределах от
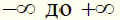
(см. Табл.1).
Таблица 1. «Расширенные» числа Фибоначчи
Эта таблица подчеркивает эстетический характер этой удивительной числовой последовательности. Удивительная симметрия такой последовательности завораживает!
Формула Кассини. Кассини – это знаменитая династия французских астрономов. Наиболее известным из них считается основатель этой династии Джованни Доменико Кассини (1625-1712). Но оказывается имя Кассини широко известно не только в астрономии, но и в математике. История науки умалчивает, почему Кассини увлекся числами Фибоначчи. Скорее всего, это было просто «хобби» великого астронома. В то время многие серьезные ученые увлекались числами Фибоначчи и золотым сечением, включая Иоганна Кеплера, современника Кассини.
Формула Кассини связывает три соседних числа Фибоначчи. Кассини первым обратил внимание на следующую закономерность, связывающую соседние числа Фибоначчи (см. Табл.1). Если взять из Табл.1 произвольное число Фибоначчи, например, F5=5 и возвести его в квадрат, то получим следующий результат: 52 = 25. А теперь сопоставим этот результат с произведением двух соседних чисел Фибоначчи F4=3 и F6=8, которые окружают число F5=5, то есть, 3 х 8=24. Мы обнаруживаем, что сравниваемые числа отличаются на 1, то есть,
52 - 3 х 8 =+1.
Проделаем то же самое с «тройкой» следующих чисел Фибоначчи 5,8,13, то есть, сначала возведем среднее число Фибоначчи F6=8 в квадрат (82=64), а после чего сопоставим этот результат с произведением двух соседних к F6=8 чисел Фибоначчи 5 и 13 (5 х 13=65), которые окружают число 8. К нашему удивлению, мы обнаруживаем, что сравниваемые числа тоже отличаются на 1, то есть,
82 - 5 х 13= -1
При этом, однако, полученная разность равна (-1).
Далее имеем: 132 - 8 х 21 = 1; 212 - 13 х 34 = – 1 и т.д. То же самое справедливо и для чисел Фибоначчи с отрицательными индексами F-n, взятыми из Табл.1.
В результате этих достаточно простых рассуждений Кассини обнаружил удивительную закономерность, которую можно сформулировать так:
Квадрат некоторого числа Фибоначчи Fn всегда отличается от произведения двух соседних чисел Фибоначчи Fn-1 и Fn+1, которые его окружают, на 1, причем знак этой единицы зависит от аргумента n числа Фибоначчи Fn; если индекс n является четным числом, то число 1 берется с минусом, а если нечетным, то с плюсом.
Это удивительное свойство чисел Фибоначчи вызывает благоговейный трепет, если представить себе, что она справедлива для любого значения
n (напомним, что
n может принимать любое значение для целого числа в пределах от
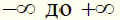
), и истинное эстетическое наслаждение, потому что чередование +1 и –1 в процессе вычисления указанной разности вызывает неосознанное чувство ритма и гармонии.
Формула Кеплера. Считается, что Кеплер первым установил следующее соотношение, связывающее числа Фибоначчи с «золотой пропорцией»: предел отношения соседних чисел Фибоначчи Fn:Fn-1 при устремлениим индекса n к бесконечности равен «золотой пропорции». Это означает, что числа Фибоначчи тесно связаны с важнейшей «гармонической пропорцией» Природы и поэтому также выражают «гармонию Мироздания».
Числа Фибоначчи в природе
Прямоугольники Фибоначчи. Используем числа Фибоначчи: 1,1,2,3,5,8,13,... для построения прямоугольников определенного вида (Рис.16). Начнем с квадрата со стороной 1. Возьмем два таких квадрата со стороной 1 (площадь каждого из них равна 1) и сложим их вместе. В результате образуется прямоугольник размером 2 х 1, называемый «двойным квадратом». Затем на большей стороне «двойного квадрата» построим новый квадрат размером 2 х 2. В результате получим прямоугольник размером 3 х 2. На большей стороне этого прямоугольника построим новый квадрат размером 3 х 3; в результате получим новый прямоугольник размером 5 х 3. Продолжая этот процесс, мы будем последовательно получать прямоугольники (Рис.16), в которых стороны являются соседними числами Фибоначчи.
Рис.16. Прямоугольники Фибоначчи
Такие прямоугольники мы будем называть прямоугольниками Фибоначчи.
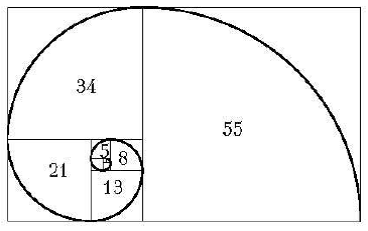
Спираль Фибоначчи. А теперь в каждом из квадратов, образующих прямоугольник Фибоначчи, проведем дугу, представляющую собой четверть окружности. Соединяя эти дуги, мы получим некоторую кривую, которая напоминает по форме спираль (Рис.17). Строго говоря, эта кривая не является спиралью с математической точки зрения, но она является очень хорошей аппроксимацией спиралей, которые широко встречаются в природе. В дальнейшем кривую на Рис.17 мы будем называть спиралью Фибоначчи.
Рис.17. Спираль Фибоначчи
Великий поэт и естествоиспытатель Гете считал спиральность одним из характерных признаков всех живых организмов, проявлением самой сокровенной сущности жизни. Спирально закручиваются усики растений и рога барана, по спирали происходит рост тканей в стволах деревьев, по спирали расположены семечки в подсолнечнике. Каждый из нас много раз восхищался формой морских раковин, которые также построены по спиралевидному закону. Но ведь и наша Галактика также имеет спиралевидную форму! Примером использования спирали Фибоначчи является, например, формы раковины наутилуса (Рис.18).
Рис.18. Спираль наутилуса
Филлотаксис и числа Фибоначчи. Как известно, числа Фибоначчи и Люка лежат в основе ботанического «закона филлотаксиса» [12]. Согласно этому закону число левых и правых спиралей на поверхности так называемых филлотаксисных объектов (сосновой шишки, ананаса, кактуса, головки подсолнечника и т.д.) описывается отношениями соседних чисел Фибоначчи, то есть:
Fn:Fn-1: 2:1, 3:2, 5:3, 8:5, 13:8, 21:13, ... (15)
Эти отношения характеризуют «симметрию» филлотаксисного объекта. При этом для каждого филлотаксисного объекта характерно свое отношение соседних чисел Фибоначчи, которое называется порядком симметрии [12].
На Рис.19 изображены примеры таких объектов (кактус, головка подсолнечника, эхинецея, головка цветной капусты, ананас, сосновая шишка), в которых закон филлотаксиса выражается своим порядком симметрии, образуемым отношениями соседних чисел Фибоначчи. То есть, в каждом из таких ботанических объектов семена или мелкие части объектов на их поверхности располагаются на пересечении левых и правых спиралей; при этом отношение числа левых и правых спиралей всегда равно одному из отношений (15) двух соседних чисел Фибоначчи.
Рис.19. Филлотаксисные структуры: (а) кактус; (b) головка подсолнечника; (c) эхинецея; (d) цветная капуста; (e) ананас; (f) сосновая шишка
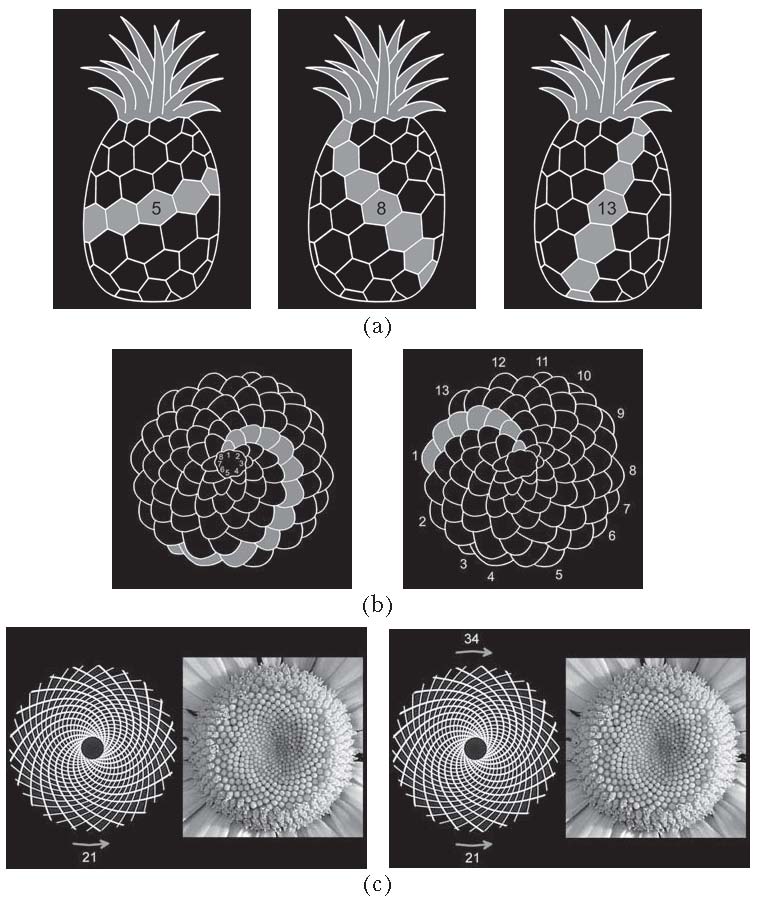
На Рис.20 изображены геометрические модели филлотаксисных структур, которые дают образное представление об этом уникальном ботаническом явлении.
Рис.20. Геометрические модели филлотаксисных структур:
(а) ананас; (b) сосновая шишка; (c) ромашка
Таким образом, строгую математику мы находим и в расположении листьев на стеблях растений, лепестков на цветке розы, в спиралевидном расположении семян в сосновой шишке, головке подсолнечника, ананасе и кактусе. И эта закономерность математически выражается числами Фибоначчи и золотой пропорцией! И мы снова и снова убеждаемся в том, что все в природе подчинено единому плану, единому закону - «закону золотого сечения» – и раскрыть и объяснить этот фундаментальный закон природы во всех его проявлениях и есть главная задача науки.
Числа Фибоначчи в современной математике
Фибоначчи-ассоциация. Огромное влияние на развитие современной «теории чисел Фибоначчи» оказало учреждение в 1963 г. математической Фибоначчи-ассоциации, которая с 1963 г. начала издавать ежеквартальный математический журнал The Fibonacci Quarterly. Одним из основателей Фибоначчи Ассоциации и The Fibonacci Quarterly был американский математик Вернер Хоггатт (Verner Emil Hoggatt) (1921-1981), профессор San Jose State University (США).
Вернер Хоггатт (Verner Emil Hoggatt) (1921-1981)
В 1969 году издательство "Houghton Mifflin" опубликовало книгу Вернера Хоггатта "Fibonacci and Lucas Numbers" [3], которая до сих пор считается одной из лучших книг в этой области. Вернер Хоггатт внес большой вклад в популяризацию исследований в области чисел Фибоначчи. Его последователи отмечают его продолжительную и, несомненно, выдающуюся работу профессором San Jose State University. Он руководил огромным количеством магистерских диссертаций и написал большое число статей по проблеме чисел Фибоначчи.
Другой выдающейся личностью, причастной к созданию Фибоначчи Ассоциации и учреждению The Fibonacci Quarterly, был ученый монах Брат Альфред Бруссау (Alfred Brousseau). Духовный орден, к которому принадлежал Брат Альфред Бруссау, назывался "Братья христианских школ" или просто "Христианские братья". Альфред Бруссау был принят в Орден "Христианские братья" в 1923 г. В 1930 г. он был зачислен в колледж Святой Марии в Калифорнии. Одновременно с обучением в колледже Святой Марии, Альфред Бруссау продолжал самостоятельно изучать физику и в 1937 г. он получил докторскую степень в Калифорнийском университете. Альфред Бруссау был страстным фотографом. Он сделал коллекцию, состоящую из 20000 дикорастущих растений Калифорнии.
Альфред Бруссау (Alfred Brousseau) (1907-1988)
При изучении истории создания Фибоначчи-ассоциации, которая поставила довольно странную цель – изучать числовую последовательность, открытую в 13 в. итальянским математиком Фибоначчи, возникают следующие естественные вопросы:
1. В чем причина повышенного интереса членов Фибоначчи-ассоциации и огромного количества «любителей математики» именно к числам Фибоначчи?
2. Что объединяло двух очень разных людей – математика Вернера Хоггатта и представителя духовного братства Альфреда Бруссау, когда они задумали создать Фибоначчи-ассоциацию и учредить математический журнал с необычным названием «The Fibonacci Quarterly»?
К сожалению, в кратких биографиях и работах Вернера Хоггатта и Альфреда Бруссау, выставленных на Интернете, прямого ответа на этот вопрос нет. Но мы можем попытаться дать ответ на эти вопросы косвенно, анализируя некоторые документы, в частности, фотографии, а также их книги и статьи, опубликованные на страницах The Fibonacci Quarterly и в других изданиях.
В 1969 г. журнал TIME опубликовал статью "The Fibonacci Numbers", посвященную Фибоначчи-ассоциации. В этой статье было представлено фото Альфреда Бруссау, держащего в руках кактус, который является одним из наиболее характерных "фибоначчиевых" ботанических объектов. В статье рассказывается и о других природных проявлениях этих чисел: о фибоначчиевой закономерности в размножении трутней, а также о том, что числа Фибоначчи встречаются в спиральных образованиях цветов, видимых на многих подсолнечниках, чешуйках сосновых шишек, ветвящихся узорах деревьев, и в расположении листьев на ветках деревьев.
Тем, кто изучает числа Фибоначчи, Альфред Бруссау рекомендовал "обращать внимание на поиск эстетического удовлетворения в них. Существует некоторый вид мистической связи между этими числами и Вселенной".
Но ведь на приведенной выше фотографии Вернер Хоггатт также изображен держащим в руках сосновую шишку, которая является одним из филлотаксисных ботанических объектов. Отсюда мы можем сделать предположение, что Вернер Хоггатт, как и Альфред Бруссау, верил в мистическую связь между числами Фибоначчи и Вселенной. Эта вера и объединила математика Вернера Хоггатта и ученого монаха Альфреда Бруссау и стала главным движущим мотивом для разворачивания работ по числам Фибоначчи и их приложениям в современной науке.
Но, как было установлено выше, числа Фибоначчи связаны с «золотой пропорцией» с помощью формулы Кеплера, согласно которой отношение соседних чисел Фибоначчи в пределе стремиться к «золотой пропорции». Это означает, что числа Фибоначчи, как и «золотая пропорция», являются количественными выразителями гармонии Мироздания, то есть, действительно «существует некоторый вид мистической связи между этими числами и Вселенной" (Альфред Брюссау).
Это означает, что теория чисел Фибоначчи, которая начала особенно активно развиваться с момента создания Фибоначчи-ассоциации (1963), была направлена, прежде всего, на решение задач гармонизации теоретического естествознания (ботаника, биология, физические науки), а также экономики, образования и искусства, связанной с золотым сечением и числами Фибоначчи. Но, как упоминалось, в основе теории чисел Фибоначчи [1-4] лежит «проблема гармонии», которая и объединяет в единое целое указанные выше разнородные области науки, экономики, искусства и образования, к которым приложимы числа Фибоначчи. Таким образом, анализируя причины возникновения теории чисел Фибоначчи в современной математике, мы неожиданно приходим к древнегреческому учению о числовой гармонии Мироздания, которое в современной математике оказалось воплощенным в «теории чисел Фибоначчи»! И возможно было бы правильно и справедливо назвать эту новую математическую теорию «математической теорией гармонии Природы», а не скрывать главную цель этой теории под названием «теория чисел Фибоначчи».
Роль Николая Воробьева в развитии «теории чисел Фибоначчи». Хотя создание американской Фибоначчи-Ассоциации в 1963 г. следует признать несомненной заслугой профессора Вернера Хоггатта и его соратников, но, справедливости ради, необходимо отметить, что первым из современных математиков обратил внимание на «теорию чисел Фибоначчи» выдающийся советский математик Николай Николаевич Воробьев (1925-1995). В 1961 г. он опубликовал брошюру «Числа Фибоначчи» [2], которая сыграла в развитии «теории чисел Фибоначчи», несомненно, выдающуюся роль. Эта небольшая по своему объему брошюра стала своеобразным бестселлером 20-го века. Она выдержала большое количество изданий, переведена на многие языки мира и стала настольной книгой многих советских и зарубежных ученых.
|
|
Николай Воробьёв ( 1925 - 1995) - выдающийся математик, специалист в области алгебры, математической логики и теории вероятностей, основатель советской школы в области теории игр. В этом смысле его роль уникальна: под его руководством советские математики сумели за короткое время развить математические основы теории игр буквально с самого начала ее зарождения в областях, до сих пор остающихся наиболее актуальными направлениями ее развития
|
Брошюра Воробьева [2] сыграла определяющую роль в приобщении одного из авторов настоящей статьи Алексея Стахова к тематике чисел Фибоначчи и выбора направлений исследований автора в кандидатской (1966) и докторской (1972) диссертациях. В 1974 г. Алексей Стахов встретился в Ленинграде с Н.Н. Воробьевым, рассказал ему о своих научных результатах в этой области и тот подарил ему брошюру «Числа Фибоначчи» (3-е издание, 1969 г.) с дарственной надписью «Глубокоуважаемому Алексею Петровичу Стахову с фибоначчистским приветом».
Брошюра Н.Н. Воробьева «Числа Фибоначчи» (3-е издание, 1969)
Славянская «Золотая» Группа. К началу 90-х годов стало ясно, что в славянской науке (Украина, Россия, Белоруссия, Польша) сформировалась группа активно работающих ученых - представителей различных наук и искусств, авторов весьма оригинальных публикаций в области золотого сечения. Возникла идея собрать воедино всех этих ученых и создать некоторое научное сообщество "золотоискателей". В 1992 г. в Киеве состоялся 1-й Международный семинар "Золотая пропорция и проблемы гармонии систем". Активными участниками семинара и членами организационного комитета стали: белорусский философ доктор философских наук Э.М. Сороко (Минск), украинский архитектор, доктор искусствоведения О.Я. Боднар (Львов), украинский экономист, доктор экономических наук И.С. Ткаченко, российский механик, доктор технических наук В.И. Коробко (Ставрополь), представитель украинской медицинской науки, доктор медицинских наук П.Ф. Шапаренко (Винница), украинский химик, кандидат химических наук Н.А. Васютинский (Запорожье), польский ученый и журналист Ян Гржеджельский. Эта группа ученых и составила костяк неформального объединения славянских ученых, вошедшего в историю науки под названием "Славянская "золотая" группа".
В 2003 г. эта группа была преобразована в Международный Клуб Золотого Сечения. По инициативе этого Клуба в 2005 г. в рамках Академии Тринитаризма (Россия) был организован Институт Золотого Сечения. По инициативе этого же Клуба в 2010 г. в Одессе был проведен Международный Конгресс по Математике Гармонии.
Международный Конгресс по Математике Гармонии.
С 8 по 10 октября 2010 г. в Одесском Национальном Университете им. И.И. Мечникова был проведен 1-й Международный Конгресс на тему "СОВРЕМЕННЫЕ АСПЕКТЫ МАТЕМАТИКИ ГАРМОНИИ И ЕЁ ПРИМЕНЕНИЕ В ЭКОНОМИКЕ, ЕСТЕСТВОЗНАНИИ, ТЕХНОЛОГИИ, СОЦИУМЕ И ОБРАЗОВАНИИ".
Проведению Конгресса предшествовало несколько важных событий, касающихся «математики гармонии» [25]. Прежде всего, в рамках подготовки к Конгрессу в Одесском университете был создан настенный музей «Математика гармонии в лицах», в котором с помощью живописных планшетов представлена история «математики гармонии», начиная с Пифагора, Платона, Евклида и до настоящего времни, и приведены примеры проявления "математики гармонии" в природе, науке и искусстве.
На заседаниях Конгресса (8, 9 и 10 октября) было сделано 30 докладов, касающихся различных теоретических аспектов «математики гармонии» и ее приложений в различных сферах современной науки. Прежде всего, необходимо отметить широкую географию участников Конгресса – от США, Канады, Чили, ФРГ до Украины (Одесса, Львов, Запорожье, Сумы), России (Москва, Санкт-Петербург, Саратов, Красноярск, Тюмень), Беларуси (Минск, Гомель). Участие в работе Конгресса ученых, прибывших из Тюмени и Красноярска (Коновалов и Южанников) можно считать героическим поступком, если учесть стоимость авиабилетов до Одессы. Таким же героическим поступком является участие в Конгрессе Почетного профессора Белорусского государственного университета транспорта Семенюты Н.Ф. (Гомель), если учесть, что ему свыше 80 лет и перед Конгрессом он тяжело переболел.
Характерной особенностью Конгресса явилось участие в нем специалистов широко профиля, работающих на стыке наук. Доктор философских наук Эдуард Сороко (Минск) является математиком по базовому образованию, доктор физико-математических наук Сергей Петухов (Москва) является одновременно кандидатом биологических наук, доктор философских наук Александр Волошинов (Саратов) одновременно является кандидатом физико-математических наук, доктор технических наук Александр Коновалов (Тюмень) имеет также ученую степень кандидата географических наук.
Все участники Конгресса сделали интересные доклады. Особый интерес вызвал доклад проф. Скотта Олсена (США), сделанный им на основе его книги “The Golden Section. Nature’s Greatest Secret” (2006) [18], получившей широкое признание в среде «золотосеченцев». Содержательные доклады были сделаны известными учеными в этой области – доктором философских наук Сороко (Минск), доктором искусствоведения Боднаром (Львов), доктором физико-математических наук Петуховым (Москва), доктором философских наук Волошиновым (Саратов) и другими.
Конгресс открыл научному сообществу новые имена. Прежде всего, это - доцент Сумского университета Сергей Якушко, рассказавший в своем докладе о сенсационном открытии в области химии – обнаруженной им фибоначчиевой закономерности в Периодической таблице Менделеева. Необходимо отметить доклад проф. Олега Когновицкого (Санкт-Петербург), в котором проведен глубокий анализ рекуррентных последовательностей Фибоначчи с использованием так называемого двойственного базиса, что имеет большое значение для развития теории помехоустойчивого кодирования. Прекрасные доклады были сделаны доктором технических наук Александром Коноваловым (Тюмень), кандидатом технических наук Александром Южанниковым (Красноярск), Денисом Клещевым (Россия), Александром Чечиком (Киев) и др.
С большим интересом были заслушаны доклады проф. Сергея Абачиева (Москва), доктора технических наук Валериана Владимирова (ФРГ), доктора биологических наук Елены Терешиной и др.
Особый шарм Конгрессу придало участие в нем представителей искусства, прежде всего, «звездного маэстро», композитора, исполнителя и кандидата наук в области астрофизики Леонида Тимошенко, композитора, музыканта и поэта Юрия Цымбалиста и исполнителя народных и классических песен доктора филологических наук проф. Григория Мартыненко. Импровизированный концерт, данный Тимошенко, Цымбалистом и Мартыненко после одного из пленарных заседаний Конгресса, несомненно, стал одним из наиболее ярких событий. «Звездный маэстро» Леонид Тимошенко исполнил несколько своих произведений на фортепиано экспромтом на заданные темы (например, на тему «Пифагор»), Юрий Цымбалист, в юности закончивший с отличием Черниговскую музыкальную школу, исполнил несколько своих песен (одна из них была посвящена Конгрессу). Большое впечатление произвело выступление Григория Мартыненко, который в сопровождении Цымбалиста (без всякой репетиции) исполнил украинскую, русскую и итальянскую народные песни. Когда в зале Ученого Совета университета зазвучал голос Мартыненко, то у многих сложилось впечатление, что в зале неожиданно появился народный артист Украины Анатолий Соловьяненко.
Своими решениями Конгресс четко определил задачи по развитию этого направления и его практического воплощения в современную жизнь. Создана Международная комиссия по «Математике гармонии», во главе с проф. Стаховым (Канада) и проф. Олсеном (США для координации работ по этому направлению.
10-я проблема Гильберта. В заключение этой части расскажем об истории решения 10-й проблемы Гильберта, при решении которой были использованы числа Фибоначчи. Эта история восходит к 1900 г. Летом этого года математики собрались в Париже на второй Международный конгресс математиков, в работе которого принимали участие самые знаменитые математические светила мира. Одним из них был немецкий математик, профессор Геттингенского университета Давид Гильберт (1862-1943), который сделал на Конгрессе доклад "Математические проблемы", в котором он сформулировал те проблемы, которые, по его мнению, должны определять дальнейшее развитие математики.
Доклад Гильберта является, возможно, наиболее значительной лекцией, прочитанной когда-либо математиком для математиков и посвященной проблемам математики. В своей лекции Гильберт изложил 23 главные математические проблемы, которые должны быть решены в новом столетии. Лекция Гильберта была больше, чем простое собрание математических проблем. Она отражала его философию математики и предлагала проблемы, важные с точки зрения его философии. И хотя прошло более столетия, лекция Гильберта является такой же важной и может быть прочитана с большим интересом каждым, кто интересуется математическими исследованиями.
Как известно, 10-я проблема Гильберта называется "Задачей о разрешении диофантовых уравнений" и для того, чтобы объяснить суть этой проблемы, мы должны возвратиться на 17 веков назад к античному математику Диофанту. Мы очень мало знаем о Диофанте, который считается последним великим математиком античности. Его творчество сыграло столь значительную роль в истории алгебры, что многие историки математики приложили немало усилий, чтобы определить срок его жизни. Предполагается, что он жил в середине 3-го столетия н.э. и прожил 84 года. Основным произведением Диофанта была "Арифметика". Именно это фундаментальное математическое сочинение, состоящее из 13 книг, явилось поворотным пунктом в развитии алгебры и теории чисел. Диофант поставил задачу нахождения целочисленных значений алгебраических уравнений. Такие уравнения получили название диофантовых.
В своей знаменитой лекции 1900 г. Давид Гильберт изложил 10-ю проблему следующим образом:
«Задано Диофантово уравнение с некоторым числом неизвестных и рациональными целыми коэффициентами. Необходимо придумать процедуру, которая могла определить за конечное число операций - является ли уравнение разрешимым в рациональных целых числах».
Десятая проблема Гильберта была решена молодым русским математиком Юрием Матиясевичем. Его имя стало широко известным в 1970 г., когда он завершил последний недостающий шаг в "негативном решении" десятой проблемы Гильберта.
И сейчас мы приблизились к главному – использованию Матиясевичем чисел Фибоначчи при решении 10-й проблемы Гильберта. В одной из своих работ Матиясевич написал:
«Мой следующий шаг состоял в том, чтобы рассмотреть широкий класс уравнений для двоичных слов с дополнительными условиями. Так как конечной целью всегда была 10-я проблема Гильберта, я мог бы рассматривать только такие условия, которые (при подходящем кодировании) были бы представлены Диофантовыми уравнениями. Таким путем я пришел к таким уравнениями, которые я назвал «equations in words and length» (уравнениями с ограниченными длинами серий). Приведение к таким уравнениям было основано на знаменитых числах Фибоначчи. Хорошо известно, что каждое натуральное число может быть представлено единственным образом как сумма различных чисел Фибоначчи, в которой нет двух соседних чисел Фибоначчи (так называемое представление Цекендорфа). Таким образом, мы можем рассматривать натуральные числа как двоичные слова с дополнительным условием, что в таких двоичных словах две 1 рядом не встречаются. Я изловчился показать, что при таком представлении чисел двоичными словами, как последовательности слов, так и уравнения, равные длине двух слов, могут быть выражены Диофантовыми уравнениями».
И далее:
«Благодаря моей предыдущей работе, я понимал важность чисел Фибоначчи для решения 10-й проблемы Гильберта. Вот почему в течение лета 1969 года я читал с огромным интересом третье расширенное издание популярной книги по числам Фибоначчи, написанной Н.Н. Воробьевым из Ленинграда. Кажется невероятным, что в 20-м столетии можно было найти что-то новое о числах, введенных Фибоначчи еще в 13-м столетии в связи с размножением кроликов. Однако, новое издание книги содержало, кроме традиционного материала, некоторые оригинальные результаты автора. На самом деле Воробьев получил их на четверть столетия раньше, но он никогда их не публиковал. Его результаты привлекли мое внимание сразу же, но я был еще не способен использовать их непосредственно для построения Диофантовых представлений экспоненциального типа».
Оценивая влияние научных результатов Воробьева и американского математика Джулии Робинзон, на решение 10-й проблемы Гильберта, Матиясевич написал:
«Мое оригинальное доказательство ... основывалось на теореме, доказанной в 1942 г. советским математиком Николаем Воробьевым, но опубликованной только в третьем расширенном издании его популярной книги.... После того, как я прочитал статью Джулии Робинзон, я сразу же увидел, что теорема Воробьева может быть очень полезной. Джулия Робинзон не видела 3-го издания книги Воробьева до тех пор, пока она не получила копию от меня в 1970 г. Кто мог сказать, что бы случилось, если бы Воробьев включил свою теорему в первое издание своей книги? Возможно, что 10-я проблема Гильберта была решена на десять лет раньше!»
В развитие вопроса Юрия Матиясевича, мы вправе поставить следующий вопрос: а что бы случилось, если бы итальянский математик Фибоначчи не открыл числа Фибоначчи в 13 в.? Возможно, 10-я проблема Гильберта не была бы решена до сих пор. Конечно, теорема Воробьева, использованная Юрием Матиясевичем, является важным математическим результатом, но все же главным «виновником» решения 10-й проблемы Гильберта следует признать итальянского математика Леонардо из Пизы (по прозвищу Фибоначчи). Еще в 1202 г. он опубликовал книгу “Liber abaci”, в которой ввел новую числовую последовательность - числа Фибоначчи.
Главный вывод из этих рассуждений состоит в том, что решение одной из наиболее сложных математических проблем – 10-й проблемы Гильберта – получено с использованием теории чисел Фибоначчи [2-4]. И этот факт сам по себе поднимает на высокий уровень как теорию чисел Фибоначчи [2-4], так и «математику гармонии» [25].
Литература
-
Coxeter, H. S. M. Introduction to Geometry. New York: John Wiley and Sons, 1961.
-
Воробьев Н.Н. Числа Фибоначчи. М.: Наука, 1984. (первое издание - 1961).
-
Hoggat V. E. Jr. Fibonacci and Lucas Numbers. - Boston, MA: Houghton Mifflin, 1969.
-
Vajda S. Fibonacci & Lucas Numbers, and the Golden Section. Theory and Applications. - Ellis Harwood Limited, 1989.
-
-
Стахов А.П. Введение в алогоритмическую теорию измерения. М.: Советское радио, 1977.
-
Стахов А.П. Коды золотой пропорции. М.: Радио и связь, 1984.
-
Сороко Э.М. Структурная гармония систем. Минск: Наука и техника, 1984.
-
Grzedzielski Jan. Energetycno-geometryczny kod Przyrody. Warszawa: Warszwskie centrum studenckiego ruchu naukowego, 1986 (in Polen).
-
Васютинский Н.А. Золотая пропорция. М.: Молодая Гвардия», 1990.
-
Шевелев И.Ш., Марутаев М.А., Шмелев И.П. Золотое сечение. Три взгляда на гармонию природы. М.: Стройиздат, 1990.
-
Боднар О.Я. Золотое сечение и неевклидова геометрия в природе и искусстве. Львов: Свит, 1994.
-
Dunlap R.A. The Golden Ratio and Fibonacci Numbers. World Scientific, 1997.
-
Коробко В.И. Золотая пропорция и проблемы гармонии систем. М.: Изд-во Ассоциации строительных вузов стран СНГ, 1998.
-
Шевелев И.Ш. Метаязык живой природы. М.: Воскресенье, 2000.
-
Kappraff Jay. Connections. The geometric bridge between Art and Science. Second Edition. Singapore, New Jersey, London, Hong Kong: World Scientific, 2001.
-
Kappraff Jay. “Beyond Measure. A Guided Tour Through Nature, Myth and Number”. Singapore, New Jersey, London, Hong Kong: World Scientific, 2002.
-
Olsen Scott. The Golden Section: Nature’s Greatest Secret. New York: Walker Publishing Company, 2006.
-
Стахов А., Слученкова А., Щербаков И. Код да Винчи и ряды Фибоначчи. Санкт-Петербург: Питер, 2006.
-
Шевелев И.Ш. Основы гармонии. Визуальные и числовые образы реального мира. М.: Луч, 2009.
-
-
Аракелян Грант. Теория ЛМФ и принцип золотого сечения. В 4 частях. Академия Тринитаризма, 2011 (электронная публикация).
-
Григорьев Ю., Мартыненко Г. Типология последовательностей Фибоначчи: Теория и приложения. Введение в математику гармонии. LAMBERT Academic Pudlishing Gmbh & Co.KG. Saarbruecken, Germany, 2012.
-
Волошинов А. В. Математика и искусство. М., Просвещение, 2000.
-
Stakhov A.P. The Mathematics of Harmony. From Euclid to Contemporary Mathematics and Computer Science. New Jersey, London, Singapore, Hong Kong: World Scientific, 2009.
-
Шестаков В.П. Гармония как эстетическая категория. М.: Наука, 1973.
-
Пьер Тейяр де Шарден. Феномен человека. Перевод и примечания Н.А.Садовского - М.: "Прогресс", 1965.
-
Дарио Салас Соммэр. Мораль XXI века. М.: Издательский дом «София», 2004.
-
Дарио Салас Соммэр. Развитие внутреннего мира. Москва: Научная книга, 2008.
-
Дарио Салас Соммэр, От Золотой Математики к Золотому Поведению //«Академия Тринитаризма», М., Эл № 77-6567, публ.15105, 20.02.2009
-
Дарио Салас Соммэр, А.П. Стахов, «Золотая» Герметическая Философия //«Академия Тринитаризма», М., Эл № 77-6567, публ.15144, 09.03.2009
-
Клайн М. Математика. Утрата определенности (пер. с англ.). Москва: Мир, 1984.
-
Колмогоров А.Н. Математика в ее историческом развитии. М.: Наука, 1991.
-
-
Dimitrov Vladimir. A new kind of social science. Study of self-organization of human dynamics. Morrisville Lulu Press, 2005.
-
Herz-Fischler, Roger. A Mathematical History of the Golden Number. New York: Dover Publications, Inc., 1998.
-
Петухов С.В. Матричная генетика, алгебры генетического кода, помехоустойчивость. Москва-Ижевск: НИЦ «Регулярная и хаотическая динамика», 2008.
-
Лосев А. История философии как школа мысли. Коммунист, 1981, №1.
-
Веннинджер М. Модели многогранников. Пер. с англ. М.: Мир, 1974.
-
Stakhov A.P. The Mathematics of Harmony: Clarifying the Origins and Development of Mathematics // Congressus Numerantium, 193, 2008, 5-48.
-
Клейн Ф. Лекции об икосаэдре и решении уравнений пятой степени. М.: Наука, 1989.
-
Гика Матила. Эстетика пропорций в природе и искусстве (пер. с фр.). Москва: Издательство Академии Архитектуры , 1936.
-
Гримм Г.Д. Пропорциональность в архитектуре. Ленинград-Москва: ОНТИ, 1935.
-
Gardner Martin. Mathematics, Magic and Mystery. New York: Publishing House “Dover”, 1952.
-
Пойа Д. Математическое открытие (перевод с англ.). М.: Наука, 1970. (английское издание, том 1, 1962, том 2, 1965)
-
-
Vera W. de Spinadel. From the Golden Mean to Chaos. Nueva Libreria, 1998 (second edition, Nobuko, 2004).
-
Gazale Midhat J. Gnomon. From Pharaohs to Fractals. Princeton, New Jersey: Princeton University Press, 1999 (Русский перевод: Мидхат Газале. Гномон. От фараонов до фракталов. Москва-Ижевск: Институт компьютерных исследований, 2002.)
-
Татаренко А.А. Золотые

– гармонии и

– фракталы — суть
солитоно-подобного Тm – cтруктурогенеза мира // «Академия
Тринитаризма», М., Эл № 77-6567, публ.12691, 09.12.2005
-
Аракелян Грант. Числа и величины в современной физике. Ереван: Изд. АН, 1989.
-
Шенягин В.П. «Пифагор, или Каждый создает свой миф» - четырнадцать лет с момента первой публикации о квадратичных мантиссовых s-пропорциях // «Академия Тринитаризма», М., Эл № 77-6567, публ.17031, 27.11.2011
-
Falcon Sergio, Plaza Angel. On the Fibonacci k-numbers Chaos, Solitons & Fractals, Volume 32, Issue 5, June 2007 : 1615-1624.
-
-
A. Stakhov, S. Aranson, “Hyperbolic Fibonacci and Lucas Functions, “Golden” Fibonacci Goniometry, Bodnar’s Geometry, and Hilbert’s Fourth Problem.” Applied Mathematics, 2011, No.1 (January), No.2 (February), No.3 (March).
-
Стахов, А.П. Формулы Газале, новый класс гиперболических функций Фибоначчи и Люка и усовершенствованный метод «золотой» криптографии // «Академия Тринитаризма», М.,Эл № 77-6567, публ.14098, 21.12.2006
-
-
-
-
-
G. Bergman, A number system with an irrational base // Mathematics Magazine, 1957, No 31: 98-119.
-
A.P. Stakhov, “The Golden Section in the Measurement Theory,” Computers & Mathematics with Applications, 1989, Vol. 17, No 4-6, 613-638.
-
A.P. Stakhov, “Generalized golden sections and a new approach to geometric definition of a number. Ukrainian Mathematical Journal, vol. 56, 2004:-1143 – 1150 (Russian).
-
A.P. Stakhov, “Brousentsov’s ternary principle, Bergman’s number system and ternary mirror-symmetrical arithmetic” // The Computer Journal, 2002, Vol. 45, No. 2, 221-236.
-
A.P. Stakhov, “A generalization of the Fibonacci Q-matrix” // Reports of the National Academy of Sciences of Ukraine, 1999, No 9, 46-49.
-
-
A.P. Stakhov, The Mathematics of Harmony: Clarifying the Origins and Development of Mathematics // Congressus Numerantium, 193, 2008, 5-48.
-
. Stakhov, “The “golden” matrices and a new kind of cryptography.” Chaos, Solitons & Fractals 2007, Volume 32, Issue 3, 1138-1146.
-
A. Stakhov, S. Aranson. “Golden” Fibonacci Goniometry. Fibonacci-Lorentz Transformations, and Hilbert’s Fourth Problem. Congressus Numerantium, 193 (2008), 119-156.
-
A.P. Stakhov, “The Golden Section and Modern Harmony Mathematics.” Applications of Fibonacci Numbers, Kluwer Academic Publishing, Volume 7, 1998: 393-399.
-
Стахов А. П., Ткаченко И. С. Гиперболическая тригонометрия Фибоначчи // Доклады Академии наук УССР, том 208, № 7, 1993.
-
Stakhov A., Rozin B. On a new class of hyperbolic function // Chaos, Solitons & Fractals, 2005, Vol. 23, Issue 2, 379-389.
Стахов А.П. Обобщенные золотые сечения и новый подход к геометрическому определению числа. // Украинский математический журнал, 2004, Vol. 56, No. 8, 1143-1150.
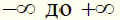 (см. Табл.1).
(см. Табл.1).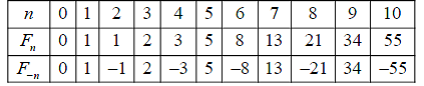
 ), и истинное эстетическое наслаждение, потому что чередование +1 и –1 в процессе вычисления указанной разности вызывает неосознанное чувство ритма и гармонии.
), и истинное эстетическое наслаждение, потому что чередование +1 и –1 в процессе вычисления указанной разности вызывает неосознанное чувство ритма и гармонии. 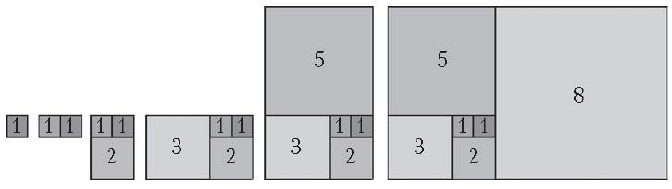







 – гармонии и
– гармонии и  – фракталы — суть
– фракталы — суть