Роль «математики гармонии» в развитии современной науки
Аннотация
Выдающийся русский философ Алексей Лосев, исследователь эстетики античности и эпохи Возрождения, в следующих словах сформулировал «золотую» парадигму древних греков: «С точки зрения Платона, да и вообще с точки зрения всей античной космологии мир представляет собой некое пропорциональное целое, подчиняющееся закону гармонического деления - золотого сечения». Новейшие открытия современной науки, основанные на Платоновых телах, золотом сечении, числах Фибоначчи: фуллерены, Нобелевская Премия – 1996; квазикристаллы, Нобелевская Премия – 2011; экспериментальное доказательство существования гармонии «золотого сечения» в квантовом мире; обнаружение фибоначчиевой закономерности в таблице Менделеева; «гипотеза Прокла» и новый взгляд на «Начала» Евклида и историю развития математики, начиная с Евклида; гиперболические фунции Фибоначчи и новая геометрическая теория филлотаксиса; треугольник Паскаля и обобщенные числа Фибоначчи; обобщенные золотые пропорции и закон структурной гармонии систем; лямбда-числа Фибоначчи как новый класс целочисленных последовательностей, обладающих уникальными математическими свойствами; «металлические пропорции» и общая теория гармонических гиперболических функций; решение четвертой проблемы Гильберта и поиск гармонических гиперболических миров Природы; "золотые" матрицы, преобразования Фибоначчи-Лоренца и «золотая» интерпретация специальной теории относительности; «золотые» геноматрицы; алгоритмическая теории измерений, коды и компьютеры Фибоначчи; системы счисления с иррациональными основаниями, троичная зеркально-симметричная арифметика и "золотая" теория чисел как новое направление в теории чисел; обобщенные матрицы Фибоначчи и новая теория кодирования; наконец, «математика гармонии» как новое междисциплинарное направление, восходящее к «Началам» Евклида, - все это «лики божественной пропорции» в современной науке, которые создают общую картину ее движения к "Золотой" Научной Революции, что в совокупности отражает одну из важнейших тенденций в развитии современной науки – возврат к Пифагору, Платону и Евклиду.
Часть IV
«Математика владеет не только истиной, но и высокой красотой – красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства».
Бертран Рассел
Предисловие
Каждому из нас не раз приходилось задумываться над тем, почему Природа способна создавать такие удивительные эстетические структуры, которые восхищают и радуют глаз. Почему художники, поэты, композиторы, архитекторы создают восхитительные произведения искусства из столетия в столетие? В чем же секрет и какие законы лежат в основе этих гармоничных созданий? Что такое «гармония»? И имеет ли она математическое выражение? Для моделирования «мира гармонии» в античном мире, прежде всего в Древней Греции, была создана математика гармонии, элементы которой возрождены в современной науке во многих книгах [1 - 25], включая книгу Alexey Stakhov “The Mathematics of Harmony. From Euclid to Contemporary Mathematics and Computer Science”, опубликованной в 2009 г. одним из наиболее престижных научных издательств мира “World Scientific” [25].
Цель настоящей публикации, предназначенной для широкой аудитории, состоит в том, чтобы популярно объяснить понятие «гармонии», которое было введено в науку на заре развития человеческой цивилизации, рассказать об истории этого направления в античный период, эпоху средневековья, эпоху Возрождения, в 19 и 20 веках, а также ввести в круг идей и приложений современной «математики гармонии», автивно развивающейся в 21 в. [25]. Конечно, «математика гармонии» - это раздел математики; поэтому полностю избежать математических формул в статье, посвященной этой математической дисциплине, авторам не удалось. Однако, «математика гармонии» - это достаточно простая (можно сказать, «элементарная») математика, в которой используются математические формулы, доступные школьникам старших классов. И авторы надеются на снисхождение наших читателей.
Статья состоит из 4-х частей:
Часть IV. Роль «математики гармонии» в развитии современной науки
Часть IV
Роль «математики гармонии» в развитии современной науки
10. Важнейшие периоды в развитии «математики гармонии»
Как упоминалось выше, для обозначения наиболее характерной особенности пифагорейской математики был введен очень удачный термин «математика гармонии» [34, 35]. При этом наибольший интерес к «математике гармонии», то есть, к идеям Пифагора, Платона и Евклида, всегда проявлялся в периоды наивысшего расцвета «человеческого духа». С учетом этого замечания в развитии «математики гармонии» можно выделить следующие важнейшие периоды.
Древнегреческий период
Условно можно считать, что этот период начинается с исследований Пифагора и Платона. Завершающим событием этого периода являются «Начала» Евклида. Согласно «гипотезе Прокла», Евклид создавал «Начала» с целью дать полную геометрическую теорию пяти «Платоновых тел», которые ассоциировались в древнегреческой науке с «гармонией Мироздания». При этом он попутно осветил некоторые новейшие достижения математики и ввел в рассмотрение «золотое сечение», которое было использовано Евклидом при создании геометрической теории «Платоновых тел».
Эпоха Возрождения
Этот период связан с именами таких выдающихся личностей этой эпохи, как Пьеро дела Франческа (1412–1492), Леон Баттиста Альберти (1404–1472), Леонардо да Винчи (1452–1519), Лука Пачоли (1445–1517), Иоганн Кеплер (1571–1630). Именно в этот период появляются две книги, которые в наибольшей степени отражали идею «гармонии Мироздания». Первая из них – это книга “Divina Proprtione” («Божественная Пропорция») (1509), написанная выдающимся итальянским математиком и ученым монахом Лукой Пачоли под непосредственным влиянием Леонардо да Винчи. Вторая книга – это книга Иоганна Кеплера “Harmonices Mundi” («Гармония мира») (1619).
Возникает вопрос: кто стимулировал возврат к идее Гармонии в эпоху Возрождения? Ответ – однозначный: христианская религия.
Морис Клайн в своей книге «Математика. Утрата определенности» (1984) [32] подчеркивает причину, по которой религия поддерживала идею математического исследование гармонии как воплощение в Природе Божественного промысла:
«Бог вложил в мир строгую математическую необходимость, которую люди постигают лишь с большим трудом, хотя их разум устроен по образу и подобию божественного разума. Следовательно, математическое знание не только представляет собой абсолютную истину, но и священно, как любая строка Священного Писания. Исследование природы – занятие столь же благородное, как и изучение Библии».
19-й век
Этот период начинается с работ французских математиков Жака Филлипа Мари Бине (1786–1856), Франсуа Эдуарда Анатоля Люка (1842–1891), немецкого поэта и философа Адольфа Цейзинга (род. в 1810 г.) и немецкого математика Феликса Клейна (1849–1925).
О вкладе Феликса Клейна в развитие «додекаэдро-икосаэдрической идеи» мы упоминали выше.
Адольф Цейзинг. В 19-м веке мы встречаем еще одного исследователя, который пытается возродить золотое сечение в эстетике. Речь идет об исследованиях немецкого поэта Адольфа Цейзинга (род. в 1810 г.). В 1854 г. он опубликовал книгу «Neue Lehre von den Proportionen des menschlichen Körpers aus einem bisher unerkannt gebliebenen, die ganze Natur und Kunst durchdringenden morphologischen Grundgesetze entwickelt». Это сочинение упрочило за Цейзингом место в истории эстетических теорий. Основная мысль сочинения — развитие закона пропорциональности деления. Ежели целое приходится делить на неравные по объёму и значению части, то эстетическое впечатление получится в том случае, когда меньшая часть деления относится к большей, как большая относится к целому. Цейзинг формулирует закон пропорциональности следующим образом:
«Деление целого на неравные части пропорционально, когда отношение частей целого между собой то же, что и отношение их к целому, т. е. то отношение, которое дает золотое сечение».
Жак Бине. Бине ввел в рассмотрение математическую формулу, которая выражает «расширенные» числа Фибоначчи (см. Табл.1) через «золотую пропорцию»
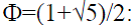
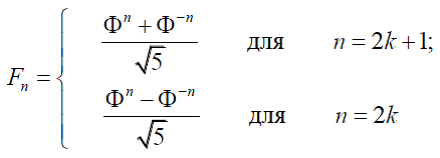
(16)
где k=0,±1,±2,±3,….
Заметим, что формула (16) относится к разряду самых удивительных формул математики. Напомним, что расширенные числа Фибоначчи
Fn - это целые числа (см. Табл.1). В то же время числа
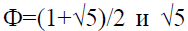
- это иррациональные числа. Именно поэтому формула (16), которая выражает целые числа в виде комбинации иррациональных чисел
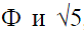
, кажется нам чем-то невообразимым, недоступным человеческому разуму. Но в этом и состоит сила математики, которая с помощью одной формулы позволяет выразить глубочайшую научную информацию, недоступную нашему пониманию. Статья полностью удовлетворяет «принципу математической красоты» Дирака и поэтому можно надеяться, что эта формула может возникнуть в некоторых математических моделях Природы, что и произошло на самом деле в конце 20 в.
Анатоль Люка. Люка ввел в рассмотрение числа Люка, которые вычисляются по той же рекуррентной формуле, что и числа Фибоначчи, но при других начальных условиях:
Ln+1= Ln+ Ln-1; L1=1, L3=3 (17)
Рекуррентная формула (17) порождает следующую числовую последовательность:
Ln : 1, 3, 4, 7, 11, 18, 29, ... (18)
Заслуга Бине и Люка состоит в том, что их исследования стали той стартовой площадкой, с которой во второй половине 20 в. начала свою научную деятельность математики-фибоначчичты в Канаде, СССР, США, Англии и других странах [1 - 4].
Первая половина 20-го века
В первой половине 20 в. развитие «золотой» парадигмы древних греков связано с именами французского исследователя Матилы Гика [42], российского профессора архитектуры Г.Д. Гримма (1865–1942) [43], и классика русской религиозной философии Павла Флоренского (1882–1937).
Матила Гика. В первой половине 20-го века большой интерес в эстетической литературе вызвала книга «Эстетика пропорций в природе и искусстве», написанная французским исследователем Матилой Гика. На русском языке книга опубликована в 1936 г. [42]. В этой книге Гика исследует свойства «божественной пропорции» и основанных на ней геометрических фигур.
Г.Д. Гримм. В теории архитектуры хорошо известна книга «Пропорциональность в архитектуре», опубликованная русским архитектором проф. Г. Д. Гриммом в 1935 г. [43]. Цель книги сформулирована во «Введении» следующим образом:
«Ввиду исключительного значения Золотого Сечения в смысле такого пропорционального деления, которое устанавливает постоянную связь между целым и его частями и даёт постоянное между ними соотношение, недостигаемое никаким другим делением, схема, основанная на нём, выдвигается как нормативная на первое место и принята нами в дальнейшем как при проверке основ пропорциональности исторических памятников, так и современных сооружений... Считаясь с этим общим значением Золотого Сечения во всех проявлениях архитектурной мысли, теорию пропорциональности, основанную на делении целого на пропорциональные части, отвечающие членам геометрической прогрессии Золотого Сечения, следует признать основой архитектурной пропорциональности вообще».
Исследования Павла Флоренского. В 20-х годах 20 в. Флоренский пишет работу «У водоразделов мысли», третья глава которой посвящена «золотому сечению». Вот её краткий набросок: «Форма и организация (Понятие формы. Целое. Divins sectio. Золотое сечение. Целое во времени. Организация времени. Циклы развития. Signatura rerum. Формула формы). Эдуард Сороко в книге [8] следующим образом оценивает эту работу Флоренского:
«Ставилась задача аналитически вывести состояния устойчивости целого, находящегося в поле действия противоположно ориентированных сил. Проект ее решения был задуман по сути дела как попытка осветить золотое сечение в той его субстанциональной основе, которая обнаруживает себя не только в серии экспериментальных наблюдений природы, но и на более глубоких уровнях ее познания, в условиях проникновения в диалектику движения, в самую сущность вещей».
25 ноября 1937 года, то есть в день 20-й годовщины Великой Октябрьской Социалистической Революции,
особой тройкой НКВД Ленинградской области Павел Флоренский был приговорён к высшей мере наказания и расстрелян
Этюды Шопена в освещении золотого сечения. Любое музыкальное произведение имеет временное протяжение и делится некоторыми вехами ("эстетическими вехами") на отдельные части, которые обращают на себя внимание и облегчают восприятие целого. Этими вехами могут быть динамические и интонационные кульминационные пункты музыкального произведения. Существуют ли какие-либо закономерности возникновения "эстетических вех" в музыкальном произведении? Попытка ответить на этот вопрос была предпринята русским композитором Л. Сабанеевым. В статье "Этюды Шопена в освещении золотого сечения" (1925 г.) он показывает, что отдельные временные интервалы музыкального произведения, соединяемые "кульминационным событием", как правило, находятся в соотношении золотого сечения.
Анализ огромного числа музыкальных произведений позволил Сабанееву сделать вывод о том, что организация музыкального произведения построена так, что его кардинальные части, разделенные вехами, образуют ряды золотого сечения. Такая организация произведения соответствует наиболее экономному восприятию массы отношений и поэтому производит впечатление наивысшей "стройности" формы. По мнению Сабанеева, количество и частота использования золотого сечения в музыкальной композиции зависит от "ранга композитора". Наиболее высокий процент совпадений отмечается у гениальных композиторов, то есть"интуиция формы и стройности, как это и следует ожидать, наиболее сильна у гениев первого класса".
По наблюдениям Сабанеева, в музыкальных произведениях различных композиторов обычно констатируется не одно золотое сечение, сопряженное с происходящим возле него "эстетическим событием", а целая серия подобных сечений. Каждое такое сечение отражает свое музыкальное событие, качественный скачок в развитии музыкальной темы. В изученных им 1770 сочинениях 42 композиторов наблюдалось 3275 золотых сечений; количество произведений, в которых наблюдалось хотя бы одно золотое сечение, составило 1338. Наибольшее количество произведений, в которых имеется золотое сечение, у Аренского (95%), Бетховена (97%), Гайдна (97%), Моцарта (91%), Скрябина (90%), Шопена (92%), Шуберта (91%).
Наиболее детально были изучены Сабанеевым все 27 этюдов Шопена. В них обнаружено 154 золотых сечения; всего в трех этюдах золотое сечение отсутствовало. В некоторых случаях строение музыкального произведения сочетало в себе симметричность и золотое сечение одновременно; в этих случаях оно делилось на несколько симметричных частей, в каждой из которых появлялось золотое сечение. У Бетховена также сочинения делятся на две симметричные части, а внутри каждой из них наблюдается проявление золотого сечения.
Вторая половина 20 века и 21-й век
Во второй половине 20 в. интерес к этому направлению возрастает во всех сферах науки, в том числе, и в математике. В области математики наиболее яркими представителями этого направления стали канадский геометр Гарольд Коксетер (1907 - 2003) [1], советский математик Николай Воробьев (1925–1995) [2], американский математик Вернер Хоггатт (1921–1981) [3], английский математик Стефан Вайда [4] и др.
Возрождение идеи гармонии в современной науке определялось новыми научными реалиями. Проникновение Платоновых тел, «золотого сечения» и чисел Фибоначчи во все сферы теоретического естествознания (кристаллография, химия, астрономия, наука о Земле, квантовая физика, ботаника, биология, геология, медицина, генетика и др.), а также в информатику и экономические науки и стало главной причиной возрождения интереса к античной идее гармонии в современной науке и стимулом для развития «математики гармонии» [1 - 25].
11. Новые рекуррентные числовые последовательности и новые математические константы для гармонических структур
Основная особенность «математики гармонии»
Чтобы понять суть «математики гармонии» и определить ее место в системе математических наук, мы обратимся к мнению выдающегося украинского математика академика Юрия Митропольского. В своем отзыве [46] он написал следующее:
«Возникает вопрос, какое место в общей теории математики занимает созданная Стаховым Математика Гармонии? Мне представляется, что в последние столетия, как выразился когда-то Н.И. Лобачевский, «математики все свое внимание обратили на высшие части Аналитики, пренебрегая началами и не желая трудиться над обрабатыванием такого поля, которое они уже раз перешли и оставили за собою». В результате между «элементарной математикой», лежащей в основе современного математического образования, и «высшей математикой» образовался разрыв. И этот разрыв, как мне кажется, и заполняет Математика Гармонии, разработанная А.П. Стаховым. То есть «Математика Гармонии» - это большой теоретический вклад в развитие прежде всего «элементарной математики», и отсюда вытекает важное значение «Математики Гармонии» для математического образования».
Таким образом, согласно Митропольскому, «математика гармонии» заполняет разрыв между «элементарной математикой» и «высшей математикой».
Но что такое «элементарная математика»? В русском языке словосочетание «элементарная математика» вызывает ощущение чего-то очень простого, школьного, недостойного внимания математика. Однако в английском языке слово «elementary» означает первоначальный, первичный, фундаментальный. Такой смысл это слово имеет, когда мы говорим Euclid’s «Elements» («Начала» Евклида) или «elementary particles» (элементарные частицы, которые составляют структурную первооснову материи). При такой трактовке прилагательного «элементарный» словосочетание «элементарная математика» необходимо понимать как раздел математики, содержащий в себе исходные, фундаментальные понятия и теории математики, которые лежат в основе «высшей математики». Именно поэтому «математика гармонии», в которой получены новые математические результаты, касающиеся «элементарной математики», по мнению Митропольского, - «это большой теоретический вклад в развитие прежде всего «элементарной математики».
Отличительная особенность «математики гармонии» состоит в том, что предметом ее изучения являются математические понятия и разделы, которые для «высшей математики», на первый взгляд, никакого интереса не представляют. К числу таких понятий относятся, например, обобщенные числа Фибоначчи и обобщенные золотые пропорции, гиперболические функции Фибоначчи, новые позиционные системы счисления и т.д. Но именно изучение этих «элементарных понятий» привело к созданию «геометрии Боднара» [12] и оригинальному решению 4-й проблемы Гильберта [68] и выдвинуло перед теоретическим естествознанием задачу поиска новых гиперболических миров Природы, а перед информатикой задачу создания принципиально новых компьютеров.
Треугольник Паскаля и р-числа Фибоначчи
Что такое треугольник Паскаля? Триста пятьдесят лет назад великий французский математик и физик Блез Паскаль (1623-1662) придумал специальный инструмент для определения биномиальных коэффициентов, в котором биномиальные коэффициенты расположены в виде треугольной таблицы следующего вида:
Рис. 25. Треугольник Паскаля
В «треугольнике Паскаля» все боковые коэффициенты равны 1, а любой коэффициент внутри «треугольника Паскаля» равен сумме двух биномиальных коэффициентов, расположенных в верхней строке и находящихся симметрично слева и справа по отношению от вычисляемого коэффициента.
Треугольник Паскаля широко используются в различных разделах математики, информатики и других науках. По существу, это – один из фундаментальных и наиболее эстетичных математических объектов, лежащих в основе точных наук. Американский математик, писатель и популяризатор науки
Мартин Гарднер (
1914 -
2010) высоко оценил треугольник Паскаля [44]:
«Треугольник Паскаля так прост, что выписать его сможет даже десятилетний ребенок. В то же время он таит в себе неисчерпаемые сокровища и связывает воедино различные аспекты математики, не имеющие на первый взгляд между собой ничего общего. Столь необычные свойства позволяют считать треугольник Паскаля одной из наиболее изящных схем во всей математике».
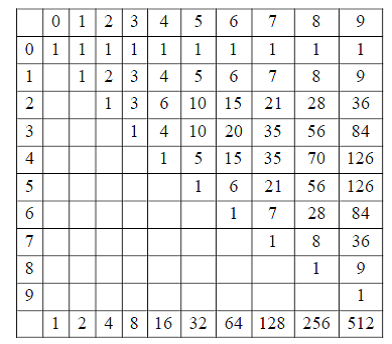
А теперь расскажем об одной «тайне» треугольника Паскаля, раскрытой совсем недвно, – его связи с числами Фибоначчи. Существует много различных форм представления треугольника Паскаля. Одна из них – это его представление в виде таблицы, напоминающей прямоугольный треугольник (см. Табл.3). Такая таблица биномиальных коэффициентов называется прямоугольным треугольником Паскаля [6].
Таблица 3. Прямоугольный треугольник Паскаля
Если просуммировать биномиальные коэффициенты n-го столбца рассматриваемого треугольника Паскаля, то мы получим двоичное число 2n. Если это сделать для всех столбцов, начиная с нулевого, то мы получим широко известную «двоичную последовательность»:
1,2,4,8,16,32,64, …, 2n (19)
Эти числа расположены в нижней строке Табл.3.
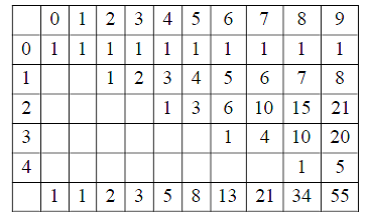
А теперь сдвинем каждую строку исходного треугольника Паскаля (Табл.3) на один столбец вправо относительно предыдущей строки. В результате такого преобразования мы получим некоторый «деформированный» треугольник Паскаля (Табл.4), который мы будем называть 1-треугольником Паскаля.
Если теперь просуммировать биномиальные коэффициенты 1-треугольника Паскаля по столбцам, то, к нашему изумлению, мы обнаружим, что такое суммирование приведет нас к числам Фибоначчи (см. нижнюю строку Табл.4).
Таблица 4. 1-треугольник Паскаля
Эта “тайна» треугольника Паскаля была раскрыта во второй половине 20 в. несколькими математиками независимо друг от друга. Считается, что первым это сделал известный американский математик и популяризатор науки Джордж Пойа (1887-1985) [45]. Следует отметить, что этот предельно простой математический результат, который, как говорится, «лежал на поверхности», в течение нескольких столетий оставался «тайной» как для Блеза Паскаля, так и для других математиков, которые соприкасались с треугольником Паскаля и числами Фибоначчи.
Но на этом сюрпризы с треугольником Паскаля не заканчиваются. Рассмотрим ситуацию, когда в исходном треугольнике Паскаля (Табл.3) мы сдвигаем биномиальные коэффициенты каждой строки на p столбцов вправо относительно предыдущей строки, где p может принимать значения из множества {0,1,2, 3, ...}. Полученный таким путем «деформированный» треугольник Паскаля мы будем называть p-треугольником Паскаля [6].
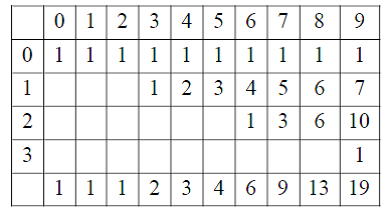
Рассмотрим, например, p-треугольник Паскаля, соответствующий случаю p=2 (Табл. 5).
Таблица 5. 2-треугольник Паскаля
Если теперь просуммировать по столбцам биномиальные коэффициенты 2- треугольника Паскаля, то в результате мы получим новую рекуррентную числовую последовательность, представленную в нижней строке Табл.5.
Легко усмотреть следующую математическую закономерность в этой числовой последовательности, которую можно выразить с помощью рекуррентной формулы:
F2(n)= F2(n-1)+ F2(n-3) для n>3 (20)
При этом вычисление новой рекуррентной числовой последовательности, представленноq в нижней строке Табл.5, осуществляется при следующих начальных условиях:
F2(1)= F2(2)= F2(3)=1. (21)
Числовая последовательность, задаваемая рекуррентной формулой (20) при начальных условиях (21), называется 2-числами Фибоначчи [6].
В общем случае (произвольное p), суммируя по столбцам биномиальные коэффициенты p-треугольника Паскаля, мы получим рекуррентную числовую последовательность, которая для заданного p=0,1,2,3,… задается следующим общим рекуррентным соотношением
Fp(n)= Fp(n-1)+ Fp(n-p-1) для n>p+1 (22)
при начальных условиях
Fp(1)= Fp(2)= Fp(p+1)=1. (23)
Числовые последовательности, задаваемые формулами (22), (23), называются 2 -числами Фибоначчи [6].
Таким образом, «манипуляции» с треугольником Паскаля привели нас к небольшому математическому открытию. Мы обнаружили бесконечное количество новых числовых последовательностей, называемых p-числами Фибоначчи (p=0,1,2,3…), задаваемых рекуррентной формулой (22) при начальных условиях (23). Эти числовые последовательности включают в себя двоичную последовательность (случай p=0) и классические числа Фибоначчи (случай p=1). Эти числовые последовательности обладают рядом интересных математических свойств, а их изучение приводит к расширению классической теории чисел Фибоначчи [2 - 4]. Но самое главное, что новые числовые последовательности выражают некоторые неизвестные нам ранее свойства треугольника Паскаля, который, по мнению Гарднера, считается «одной из наиболее изящных схем во всей математике». Именно поэтому мы должны с достаточной степенью уважения отнестись к новым рекуррентным числовым последовательностям, которые представляют интерес как для комбинаторики (треугольник Паскаля), так и для «теории чисел Фибоначчи» [2 - 4].
Золотые р-пропорции
Выше в Части II было рассказано о так называемой «формуле Кеплера». Согласно этой формуле, отношение двух соседних чисел Фибоначчи в пределе
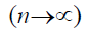
стремится к «золотой пропорции».
В работе [6] доказано, что при заданном
р=0,1,2,3,... отношение двух соседних
р-чисел Фибоначчи
Fp(
n)/
Fp(
n-1) в пределе
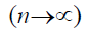
стремится к некоторой математической константе Ф
р, которая равна положительному корню следующего алгебраического уравнения:
xp+1- xp-1=0. ( 24)
Заметим, что уравнение (24) включает в себя бесконечное число алгебраических уравнений, так как каждому p соответствует свое алгебраическое уравнение типа (24). В частности, для случая p=0 уравнение (24) вырождается в тривиальное уравнение x-2=0, корень которого Ф0 =2.
Для случая p=1 уравнение (24) сводится к уравнению золотого сечения,
корнем которого является золотая пропорция. На этом основании константы Фp были названы золотыми р-пропорциями [6]. Ниже в Табл.6 приведены приближенные значения констант Фр для различных значений р.
Таблица 6. Численные значения констант Фр
Существенно подчеркнуть, что константы Фр представляют фундаментальный интерес, так как они выражают неизвестные для нас свойства треугольника Паскаля.
Этот математический результат получил высокую оценку выдающегося украинского математика, академика двух академий (РАН и Украинской Академии Наук) Юрия Алексеевича Митропольского, который в своем отзыве [46] написал:
«Давайте вдумаемся в этот результат. В течение нескольких тысячелетий, начиная с Пифагора и Платона, человечество пользовалось широко известным классическим Золотым Сечением, которое считалось единственным, уникальным и неповторимым. И вот в конце 20-го века украинский ученый Стахов обобщает эту задачу и доказывает существование бесконечного числа Золотых Сечений! И все они имеют такое же право на существование, как и классическое Золотое Сечение. Более того, Стахов показывает, что Золотые р-пропорции Фр представляют собой новый класс иррациональных чисел, которые выражают некоторые неизвестные нам до этого математические свойства треугольника Паскаля. Ясно, что такой математический результат имеет фундаментальное значение для развития современной науки и математики».
Закон структурной гармонии систем
Белорусский философ Эдуард Сороко использовал золотые р-пропорции для формулировки «закона струкурной гармонии систем», который звучит следующим образом [8]:
«Обобщенные золотые сечения суть инварианты, на основе и посредством которых в процессе самоорганизации естественные системы обретают гармоничное строение, стационарный режим существования, стуктурно-функциональную …устойчивость».
В чем же принципиальная особенность "Закона Сороко"? Начиная с Пифагора, ученые связывали понятие гармонии с классической «золотой пропорцией». "Закон Сороко" утверждает, что гармоничное состояние системы, соответствующее классической «золотой пропорции», не является единственным и что для одной и той же системы может существовать бесконечное количество "гармоничных" состояний, соответствующих различным «золотым р-пропорциям». Это – новая идея в развитии теории гармонии систем.
Q-числа Фибоначчи
Немного истории. В истории науки очень часто бывает так, что несколько ученых независимо друг от друга приходят к одному и тому же научному открытию. Современная «математика гармонии» [25] является активно развивающимся направлением современной науки и математики. В конце 20-го и начале 21-го вв. сразу несколько исследователей из разных стран – аргентинский математик Вера Шпинадель [47], французский математик Мидхат Газале [48], американский математик Джей Каппрафф [16, 17], российский исследователь Александр Татаренко [49], армянский философ и физик Грант Аракелян [50], российский исследователь Виктор Шенягин [51], испанские математики Falcon Sergio, Plaza Angel [52] и др. независимо друг от друга начали изучать новый класс рекуррентных числовых последовательностей, которые являются еще одним обобщением классических чисел Фибоначчи. Эти числовые последовательности, введенные в [53, 54] и которые мы будем называть q-числами Фибоначчи, привели к открытию нового класса математических констант, названных аргентинским математиком Верой Шпиналель «металлическими пропорциями» [47].
Рекуррентное соотношение для q-чисел Фибоначчи. Зададимся натуральным числом q=1,2,3,... и рассмотрим следующее рекуррентное соотношение:
Fq (n+2)= qFq (n+1)+Fq (n); Fq (0)=0, Fq (1)=1 (24)
Рекуррентное соотношение (24) «генерирует» бесконечное количество новых рекуррентных числовых последовательностей, так как каждому q=1,2,3,... соответствует своя числовая последовательность. Важно подчеркнуть, что их частными случаями являются некоторые числовые последовательности, получившие широкую известность в современной науке.
В частности, для случая рекуррентное соотношение (24) сводится к рекуррентному соотношению Фибоначчи, которое «генерирует» числа Фибоначчи: 0,1,1,2,3,5,8,13,21,34... Основываясь на этом факте, числовые последовательности, генерируемые рекуррентным соотношением (24), были названы q-числами Фибоначчи [53, 54].
При q=2 рекуррентное соотношение (33) сводится к рекуррентному соотношению
F2(n+2)= 2F2(n+1)+F2(n); F2(0)=0, F2(1)=1, (25)
которое «генерирует» так называемые числа Пелля: 0,1,2,5,12,29,70,...
Q-числа Фибоначчи обладают многими замечательными свойствами, подобными свойствам классических чисел Фибоначчи. Доказано, что q-числа Фибоначчи так же, как классические числа Фибоначчи, могут быть «расширены» в сторону отрицательных значений дискретной переменной n.
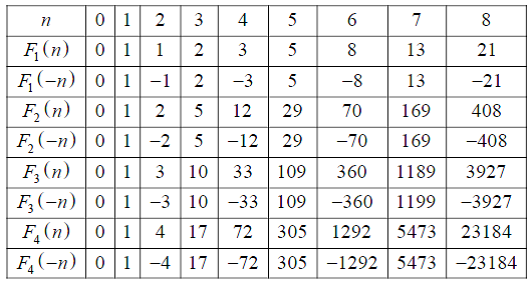
В Табл.8 приведены четыре расширенные последовательности q-чисел Фибоначчи, соответствующие значениям q=1,2,3,4.
Таблица 8. Расширенные q-числа Фибоначчи (q=1,2,3,4)
А теперь расскажем об одном новом математическом результате, полученном в работе [56]. Для этого выберем в строке F2(n) Табл.8 число F2(n=7)=169. Важно отметить, что номер этого числа n=7 является нечетным числом. А теперь рассмотрим числа и F2(n=6)=70 и F2(n=8)=408 которые окружают число F2(n=7)=169, и вычислим разность:
(169)2-70´408=28561 – 28561 = +1
Эта разность равна (+1).
А теперь выберем из другой строки F3(n) таблицы 8 число F3(n=6)=360 с четным номером n=6, а также числа F3(n=5)=109 и F3(n=7)=1189, которые его окружают, и произведем сдедующее вычисление:
(360)2 - 109´1189=12960 – 12961 = -1
К нашему удивлению, мы обнаружили, что эта разность равна (-1).
Если продолжить этот эксперимент, то мы получим, что для любого q-числа Фибоначчи Fq(n) с нечетным номером n=2k+1 подобного рода разность всегда равна (+1), а для любого q-числа Фибоначчи Fq(n) с четным номером n=2k подобная разность равна (-1). Это наблюдение приводит нас к следующему неожиданому утверждению, доказанному в [56].
Квадрат некоторого q-числа Фибоначчи Fq(n) всегда отличается от произведения двух соседних q-чисел Фибоначчи Fq(n-1) и Fq(n+1), которые его окружают, на 1, причем знак этой единицы зависит от четности числа n; если число n является четным, то 1 берется с минусом, а если нечетным, то с плюсом.
Самое любопытное, что этот математический результат может оказаться сюрпризом не только для наших читателей, но для современных математиков, специализирующихся в области теории чисел. Суть результата состоит в том, что в множесте целых чисел (которое является предметом изучения в теории чисел) обнаружено бесконечное число новых целочисленных последовательностей (q-чисел Фибоначчи), обладающих уникальными математическими свойствами. Это означает, что в рамках «математики гармонии» [25] в 21-м в. получен новый фундаментальный математический результат [56], имеющий непосредственное отношение к теории чисел – старейшей математической дисциплине.
Металлические пропорции
Изложенные ниже рассуждеия взяты из книги Веры Шпинадель [47] и статьи Алексея Стахова [55].
Если разделить обе части рекуррентного соотношения (24) на Fq-(n+1), то в результате предельного перехода (n®µ) мы получим следующее алгебраическое уравнение:
x2 - qx – 1=0 (26)
Обозначим через Фq положительный корень квадратного уравнения (26), который задается следующим выражением:
(27)
Заметим, что для случая q=1 формула (27) сводится к классической «золотой пропорции»:
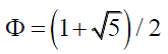
(28)
Уже этот факт должен привлечь наше внимание к формуле (27), которая является обобщением одной из самых известных математических формул (28).
Аргентинский математик Вера Шпинадель [47] назвала математические константы, задаваемые выражением (27), металлическими пропорциями.
Ясно, что количество «металлических пропорций», задаваемых (27), теоретически бесконечно, так каждому натуральному числу q=1,2,3,... соответствует своя «металлическая пропорция» типа (27).
12. Новые гиперболические миры Природы
История гиперболической геометрии
В первой четверти 19 в. было сделано выдающееся математическое открытие, которое, по мнению академика Колмогорова [33], положило начало современного периода в развитии математики. Речь идет о неевклидовой геометрии, к которой независимо друг от друга и в одно и то же время пришли российский геометр Николай Лобачевский, венгерский математик Янош Больяи и, как потом оказалось, выдающийся немецкий математик Иога́нн Карл Фри́дрих Га́усс. Но Лобачевский опередил всех. Он первым опубликовал свои результаты по новой геометрии и тем самым закрепил приоритет российкой математики в этой важном направлении в геометрии. И поэтому эта геометрия по праву называется «геометрией Лобачевского». Как-то даже не верится, что это выдающееся математическое открытие на начальном этапе было подвержено резкой критике со строны наиболее известного российского математика того периода академика М.В. Остроградского. Спасибо немецкому математику Гауссу, который дал высокую оценку работам российского геометра, которые вскоре так же высоко были оценены и другими западными математиками. А негативный отзыв академика Остроградского на новую геометрию навсегда вошел в историю науки как один из позорных случаев в истории российской математики.
Новые классы гиперболических функций
«Геометрия Лобачевского» называется также «гиперболической геометрией». Этим названием подчеркивается тот факт, что эта геометрия основана на так называемых гиперболических функциях:
sh(x)=(ex –e-x)/2; ch(x)=(ex +e-x)/2; (29)
Заметим, что основанием этих функций является число е, одна из фундаментальных математических констант, которая является также основанием натуральных логарифмов. Считается, что гиперболические функции были введены итальянским математиком Винченцо Риккати (Vincenzo Riccati) в 1757 году. Следует отметить, что интерес к гиперболическим функциям в математике резко повысился в 19 в., когда Николай Лобачевский использовал функции (29) в разработаной им неевклидовой геометрии, которая получила название гиперболической геометрии.
А теперь рассмотрим новые классы гиперболических функций, введенных в рамках «математики гармонии [25]:
Гиперболичские функции (30), (31) называются гиперболическим синусом и косинусом Фибоначчи [70,71], соответственно, а гиперболичские функции (32), (33) - гиперболическим q-синусом и q-косинусом Фибоначчи [53,55], соответственно.
В чем же состоит особенность новых классов гиперболических функций? Первая особенность состоит в том, что основанием функций (30), (31) является знаменитая «золотая пропорция» (28), а основанием функций (32), (33) - «металлические пропорции» (27). Таким образом, эти функции можно назвать «гармоническими гиперболическими функциями» на том основании, что они порождаются «золотой пропорцией» (28) и «металлическими пропорциями» (27) - новыми математическими константами, которые являются обобщением «золотой пропорции».
А теперь сравним гиперболические функции Фибоначчи (30), (31) с «формулами Бине» (16). Это сравнение приводит нас к неожиданyому заключению: «расширенные числа Фибоначчи», задаваемые «формулами Бине» (16) в дискретных точках переменной x совпадают с функциями (30), (31), то есть,
(34)
Оказывается, подобная же связь существует между функциями (32), (33) и «расширенными q-числами Фибоначчи», задаваемыми «формулами Газале» [48]:
(35)
откуда вытекает следующее соотношение, связывающее q-числа Фибоначчи с функциями (32), (33):
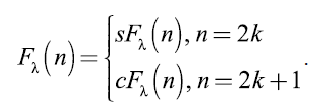
(36)
Загадка филлотаксиса и «геометрия Боднара»
Наблюдая филлотаксисные объекты в завершенном состоянии и наслаждаясь упорядоченным рисунком на их поверхности, мы всегда задаем себе вопрос: как в процессе роста на его поверхности формируются «фибоначчиевы спирали»? Эта проблема и представляет собой одну из наиболее интригующих загадок филлотаксиса. Суть ее состоит в том, что у большинства видов биоформ в процессе роста происходит изменение числовых характеристик симметрии, под которыми понимаются отношения количеств левых и правых фибоначчиевых спиралей. Известно, например, что головки подсолнечника, находящиеся на разных уровнях одного и того же стебля, имеют разные порядки симметрии: чем старше диск, тем выше порядок его симметрии. Это означает, что в процессе роста происходит закономерное изменение (возрастание) порядка симметрии, и это изменение осуществляется по закону:
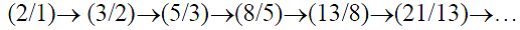
(37)
В современной науке «загадка филлотаксиса» (37) была блестяще решена украинским исследователем Олегом Боднаром [12]. Боднар доказал, что «геометрия филлотаксиса» является новым вариантом «гиперболической геометрии Лобачевского». Особенность «геометрии филлотаксиса» состоит в том, что в процессе роста филлотаксисных объектов Природа использует гиперболические функции Фибоначчи (30), (31)!
Заметим, что именно уникальное мматематическое свойство (34) является основной причиной появления «фибоначчиевых спиралей» на поверхности филлотаксисных объектов!
И здесь еще раз уместно вспомнить о «принципе математической красоты» Дирака, который нашел блестящее воплощение в «геометрии Боднара» [12]!
Оригинальное решение 4-й проблемы Гильберта
Еще одним неожиданным приложенеием функций (32), (33) является оригинальное решение 4-й проблемы Гильберта, полученное в статье [54]. Эту проблему Гильберт сформулировал так:
«Более общий вопрос, возникающий при этом, заключается в следующем: возможно ли ещё с других плодотворных точек зрения построить геометрии, которые с таким же правом могли бы считаться ближайшими к обыкновенной евклидовой геометрии...»
Таким образом, Гильберт в 4-й проблеме ставит вопрос о нахождении новых невклидовых геометрий, ближайших к евклидовой геометрии.
Оказалось, что гиперболические q-функции Фибоначчи (32), (33) открывают путь к решению этой проблемы. Число классов функций (32), (33) теоретически бесконечно. Их столько же, сколько существует натуральных чисел q=1,2,3,…. Но каждый класс таких функций «порождает» свою «гиперболическую геометрию», подобную «геометрии Боднара» [12]. Из этих рассуждений вытекает предельно простое решение 4-й проблемы Гильберта: количество новых гиперболических геометрий, которые являются «ближайшими к обыкновенной евклидовой геометрии» (Гильберт), теоретически бесконечно и все они задаются функциями (32), (33)!
13. Назад к Пифагору, Платону и Евклиду
Платоновы тела и «золотое сечение» в истории науки и культуры
Дифференциация современной науки и ее разделение на отдельные сферы не позволяют зачастую увидеть общую картину науки и основные тенденции ее развития. Однако, в науке существуют исследовательские объекты, которые объединяют разрозненные научные факты в единое целое. К разряду таких объектов можно отнести Платоновы тела и золотое сечение. Древние греки возвысили их до уровня «главных выразителей гармонии Мироздания», то есть, согласно древним грекам, эти геометрические объекты имеют отношение ко всему Мирозданию. На протяжении веков или даже тысячелетий, начиная с Пифагора, Платона, Евклида, эти геометрические объекты были предметом восхищения и поклонения выдающихся умов человечества - в эпоху Возрождения - Леонардо да Винчи, Луки Пачоли, Иоганна Кеплера, в 19 веке - Цейзинга, Люка, Бине, Клейна. В 20-м веке интерес к этим математическим объектам значительно возрос в математике, благодаря исследованиям канадского математика Гарольда Коксетера [1], советского математика Николая Воробьева [2] и американского математика Вернера Хоггатта [3], с работ которых начинается процесс «гармонизации современной математики» [57]. Развитие этого направления привело к созданию «математики гармонии» как нового междисциплинарного направления современной науки [25].
Роль Платоновых тел и «золотого сечения» в современной науке
Новейшие открытия современной науки, основанной на Платоновых телах, золотом сечении, числах Фибоначчи, и новейшие научные результаты, основанные на "гармонических достижениях» древних греков (фуллерены [58], квазикристаллы [59], новая геометрическая теория филлотаксиса [12], "золотые" геноматрицы [37], общая теория гиперболических функций [53], решение четвертой проблемы Гильберта [53, 54], алгоритмическая теории измерений и коды Фибоначчи [6], системы счисления с иррациональными основаниями [60], коды золотой р-пропорции [7, 60], "золотая" теория чисел [72], троичная зеркально-симметричная арифметика [63], обобщенные матрицы Фибоначчи [64], новая теория кодирования, основанная на матрицах Фибоначчи [65], "гипотеза Прокла» и новый взгляд на историю математики, начиная с Евклида [66], "золотые" матрицы [67], преобразования Фибоначчи-Лоренца и "золотая" интерпретация специальной теории относительности [68], наконец, "Математики Гармонии» [25, 40, 69] и т.д.) создают общую картину движения современной науки к "Золотой" Научной Революции, которая соответствует одной из важнейших тенденций в развитии современной науки – возврат к Пифагору, Платону, Евклиду.
Литература
-
Coxeter, H. S. M. Introduction to Geometry. New York: John Wiley and Sons, 1961.
-
Воробьев Н.Н. Числа Фибоначчи. М.: Наука, 1984. (первое издание - 1961).
-
Hoggat V. E. Jr. Fibonacci and Lucas Numbers. - Boston, MA: Houghton Mifflin, 1969.
-
Vajda S. Fibonacci & Lucas Numbers, and the Golden Section. Theory and Applications. - Ellis Harwood Limited, 1989.
-
-
Стахов А.П. Введение в алогоритмическую теорию измерения. М.: Советское радио, 1977.
-
Стахов А.П. Коды золотой пропорции. М.: Радио и связь, 1984.
-
Сороко Э.М. Структурная гармония систем. Минск: Наука и техника, 1984.
-
Grzedzielski Jan. Energetycno-geometryczny kod Przyrody. Warszawa: Warszwskie centrum studenckiego ruchu naukowego, 1986 (in Polen).
-
Васютинский Н.А. Золотая пропорция. М.: Молодая Гвардия», 1990.
-
Шевелев И.Ш., Марутаев М.А., Шмелев И.П. Золотое сечение. Три взгляда на гармонию природы. М.: Стройиздат, 1990.
-
Боднар О.Я. Золотое сечение и неевклидова геометрия в природе и искусстве. Львов: Свит, 1994.
-
Dunlap R.A. The Golden Ratio and Fibonacci Numbers. World Scientific, 1997.
-
Коробко В.И. Золотая пропорция и проблемы гармонии систем. М.: Изд-во Ассоциации строительных вузов стран СНГ, 1998.
-
Шевелев И.Ш. Метаязык живой природы. М.: Воскресенье, 2000.
-
Kappraff Jay. Connections. The geometric bridge between Art and Science. Second Edition. Singapore, New Jersey, London, Hong Kong: World Scientific, 2001.
-
Kappraff Jay. “Beyond Measure. A Guided Tour Through Nature, Myth and Number”. Singapore, New Jersey, London, Hong Kong: World Scientific, 2002.
-
Olsen Scott. The Golden Section: Nature’s Greatest Secret. New York: Walker Publishing Company, 2006.
-
Стахов А., Слученкова А., Щербаков И. Код да Винчи и ряды Фибоначчи. Санкт-Петербург: Питер, 2006.
-
Шевелев И.Ш. Основы гармонии. Визуальные и числовые образы реального мира. М.: Луч, 2009.
-
-
Аракелян Грант. Теория ЛМФ и принцип золотого сечения. В 4 частях. Академия Тринитаризма, 2011 (электронная публикация).
-
Григорьев Ю., Мартыненко Г. Типология последовательностей Фибоначчи: Теория и приложения. Введение в математику гармонии. LAMBERT Academic Pudlishing Gmbh & Co.KG. Saarbruecken, Germany, 2012.
-
Волошинов А. В. Математика и искусство. М., Просвещение, 2000.
-
Stakhov A.P. The Mathematics of Harmony. From Euclid to Contemporary Mathematics and Computer Science. New Jersey, London, Singapore, Hong Kong: World Scientific, 2009.
-
Шестаков В.П. Гармония как эстетическая категория. М.: Наука, 1973.
-
Пьер Тейяр де Шарден. Феномен человека. Перевод и примечания Н.А.Садовского - М.: "Прогресс", 1965.
-
Дарио Салас Соммэр. Мораль XXI века. М.: Издательский дом «София», 2004.
-
Дарио Салас Соммэр. Развитие внутреннего мира. Москва: Научная книга, 2008.
-
Дарио Салас Соммэр, От Золотой Математики к Золотому Поведению //«Академия Тринитаризма», М., Эл № 77-6567, публ.15105, 20.02.2009
-
Дарио Салас Соммэр, А.П. Стахов, «Золотая» Герметическая Философия //«Академия Тринитаризма», М., Эл № 77-6567, публ.15144, 09.03.2009
-
Клайн М. Математика. Утрата определенности (пер. с англ.). Москва: Мир, 1984.
-
Колмогоров А.Н. Математика в ее историческом развитии. М.: Наука, 1991.
-
-
Dimitrov Vladimir. A new kind of social science. Study of self-organization of human dynamics. Morrisville Lulu Press, 2005.
-
Herz-Fischler, Roger. A Mathematical History of the Golden Number. New York: Dover Publications, Inc., 1998.
-
Петухов С.В. Матричная генетика, алгебры генетического кода, помехоустойчивость. Москва-Ижевск: НИЦ «Регулярная и хаотическая динамика», 2008.
-
Лосев А. История философии как школа мысли. Коммунист, 1981, №1.
-
Веннинджер М. Модели многогранников. Пер. с англ. М.: Мир, 1974.
-
Stakhov A.P. The Mathematics of Harmony: Clarifying the Origins and Development of Mathematics // Congressus Numerantium, 193, 2008, 5-48.
-
Клейн Ф. Лекции об икосаэдре и решении уравнений пятой степени. М.: Наука, 1989.
-
Гика Матила. Эстетика пропорций в природе и искусстве (пер. с фр.). Москва: Издательство Академии Архитектуры , 1936.
-
Гримм Г.Д. Пропорциональность в архитектуре. Ленинград-Москва: ОНТИ, 1935.
-
Gardner Martin. Mathematics, Magic and Mystery. New York: Publishing House “Dover”, 1952.
-
Пойа Д. Математическое открытие (перевод с англ.). М.: Наука, 1970. (английское издание, том 1, 1962, том 2, 1965)
-
-
Vera W. de Spinadel. From the Golden Mean to Chaos. Nueva Libreria, 1998 (second edition, Nobuko, 2004).
-
Gazale Midhat J. Gnomon. From Pharaohs to Fractals. Princeton, New Jersey: Princeton University Press, 1999 (Русский перевод: Мидхат Газале. Гномон. От фараонов до фракталов. Москва-Ижевск: Институт компьютерных исследований, 2002.)
-
Татаренко А.А. Золотые Tm – гармонии и Dm – фракталы — суть солитоно-подобного Тm – cтруктурогенеза мира // «Академия Тринитаризма», М., Эл № 77-6567, публ.12691, 09.12.2005
-
Аракелян Грант. Числа и величины в современной физике. Ереван: Изд. АН, 1989.
-
Шенягин В.П. «Пифагор, или Каждый создает свой миф» - четырнадцать лет с момента первой публикации о квадратичных мантиссовых s-пропорциях // «Академия Тринитаризма», М., Эл № 77-6567, публ.17031, 27.11.2011
-
Falcon Sergio, Plaza Angel. On the Fibonacci k-numbers Chaos, Solitons & Fractals, Volume 32, Issue 5, June 2007 : 1615-1624.
-
-
A. Stakhov, S. Aranson, “Hyperbolic Fibonacci and Lucas Functions, “Golden” Fibonacci Goniometry, Bodnar’s Geometry, and Hilbert’s Fourth Problem.” Applied Mathematics, 2011, No.1 (January), No.2 (February), No.3 (March).
-
Стахов, А.П. Формулы Газале, новый класс гиперболических функций Фибоначчи и Люка и усовершенствованный метод «золотой» криптографии // «Академия Тринитаризма», М.,Эл № 77-6567, публ.14098, 21.12.2006
-
-
-
-
-
G. Bergman, A number system with an irrational base // Mathematics Magazine, 1957, No 31: 98-119.
-
A.P. Stakhov, “The Golden Section in the Measurement Theory,” Computers & Mathematics with Applications, 1989, Vol. 17, No 4-6, 613-638.
-
A.P. Stakhov, “Generalized golden sections and a new approach to geometric definition of a number. Ukrainian Mathematical Journal, vol. 56, 2004:-1143 – 1150 (Russian).
-
A.P. Stakhov, “Brousentsov’s ternary principle, Bergman’s number system and ternary mirror-symmetrical arithmetic” // The Computer Journal, 2002, Vol. 45, No. 2, 221-236.
-
A.P. Stakhov, “A generalization of the Fibonacci Q-matrix” // Reports of the National Academy of Sciences of Ukraine, 1999, No 9, 46-49.
-
-
A.P. Stakhov, The Mathematics of Harmony: Clarifying the Origins and Development of Mathematics // Congressus Numerantium, 193, 2008, 5-48.
-
. Stakhov, “The “golden” matrices and a new kind of cryptography.” Chaos, Solitons & Fractals 2007, Volume 32, Issue 3, 1138-1146.
-
A. Stakhov, S. Aranson. “Golden” Fibonacci Goniometry. Fibonacci-Lorentz Transformations, and Hilbert’s Fourth Problem. Congressus Numerantium, 193 (2008), 119-156.
-
A.P. Stakhov, “The Golden Section and Modern Harmony Mathematics.” Applications of Fibonacci Numbers, Kluwer Academic Publishing, Volume 7, 1998: 393-399.
-
Стахов А. П., Ткаченко И. С. Гиперболическая тригонометрия Фибоначчи // Доклады Академии наук УССР, том 208, № 7, 1993.
-
Stakhov A., Rozin B. On a new class of hyperbolic function // Chaos, Solitons & Fractals, 2005, Vol. 23, Issue 2, 379-389.
-
Стахов А.П. Обобщенные золотые сечения и новый подход к геометрическому определению числа. // Украинский математический журнал, 2004, Vol. 56, No. 8, 1143-1150.

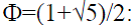
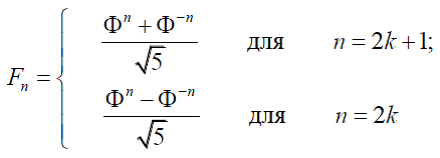 (16)
(16)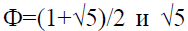 - это иррациональные числа. Именно поэтому формула (16), которая выражает целые числа в виде комбинации иррациональных чисел
- это иррациональные числа. Именно поэтому формула (16), которая выражает целые числа в виде комбинации иррациональных чисел 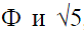 , кажется нам чем-то невообразимым, недоступным человеческому разуму. Но в этом и состоит сила математики, которая с помощью одной формулы позволяет выразить глубочайшую научную информацию, недоступную нашему пониманию. Статья полностью удовлетворяет «принципу математической красоты» Дирака и поэтому можно надеяться, что эта формула может возникнуть в некоторых математических моделях Природы, что и произошло на самом деле в конце 20 в.
, кажется нам чем-то невообразимым, недоступным человеческому разуму. Но в этом и состоит сила математики, которая с помощью одной формулы позволяет выразить глубочайшую научную информацию, недоступную нашему пониманию. Статья полностью удовлетворяет «принципу математической красоты» Дирака и поэтому можно надеяться, что эта формула может возникнуть в некоторых математических моделях Природы, что и произошло на самом деле в конце 20 в.
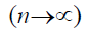 стремится к «золотой пропорции».
стремится к «золотой пропорции».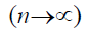 стремится к некоторой математической константе Фр, которая равна положительному корню следующего алгебраического уравнения:
стремится к некоторой математической константе Фр, которая равна положительному корню следующего алгебраического уравнения:
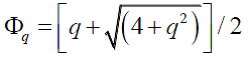
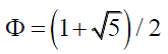 (28)
(28)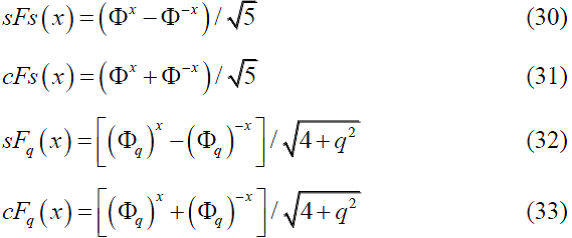
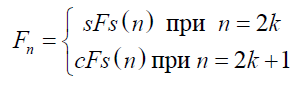
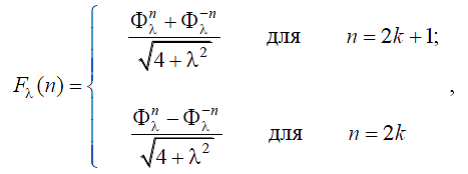
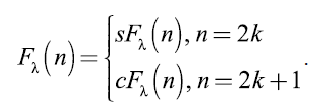 (36)
(36)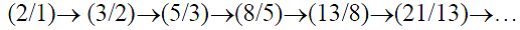 (37)
(37)